Um retângulo no plano tem vértices em , e um quadrado no plano tem seus lados paralelos aos eixos coordenados, mede por e tem seu canto inferior esquerdo na reta . Qual é a maior área possível de uma região no plano que esteja contida em ambos, e ?
Passo 1
Vamos refletir, a gente tem um retângulo. E no mesmo plano tem um quadrado muito maior que esse retângulo, que tem o vértice na reta . Olha como fica num desenho:
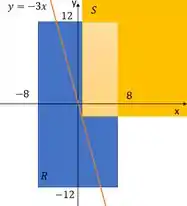
A interseção entre essas figuras é esse retângulo mais clarinho. O que a gente precisa fazer é descobrir a maior área que esse retângulo pode ter.
Para descobrir isso, a gente precisa encontrar uma função que descreve essa área e descobrir o maior valor dela.
Vamos tentar fazer isso!
Passo 2
A gente sabe que o quadrado tem o vértice na reta . Então a gente pode dizer que o vértice dele está no ponto:
Mas repara que esse ponto só pode estar dentro do retângulo. Isso significa que esse não vai ser todos os reais, mas só os valores de para quais a reta está dentro desse retângulo.
Pela localização do nosso retângulo, vemos que está entre as retas:
Substituindo esses valores de em , e isolando , achamos:
Por isso, podemos dizer que nosso está entre esses valores. Reescrevendo nosso vértice:
Passo 3
Vamos olhar uma figura nova:
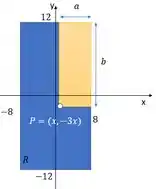
Queremos a área do retângulo menor, que podemos escrever como:
Mas quem é e ?
Olhando para figura, vemos que é um valor que está entre e a coordenada do ponto , que vale . Podemos dizer então:
Dá para fazer a mesma coisa com . É um valor que está entre e a coordenada do ponto , que vale . E aí:
Reescrevendo a área:
Passo 4
Com a expressão da área, podemos tentar descobrir o valor máximo dela. Como ela é um polinômio, o valor máximo vai acontecer nos extremos ou valores de onde . Esses serão nossos candidatos!
Vamos derivar essa função da área e igualar a zero:
Igualando a zero:
Passo 5
Nossos candidatos são:
Agora a gente sustitui eles na função da área para saber qual resulta no maior valor de :
O que resultou no maior valor foi , e a gente descobriu que a área máxima da região que o enunciado pediu é: