Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 25
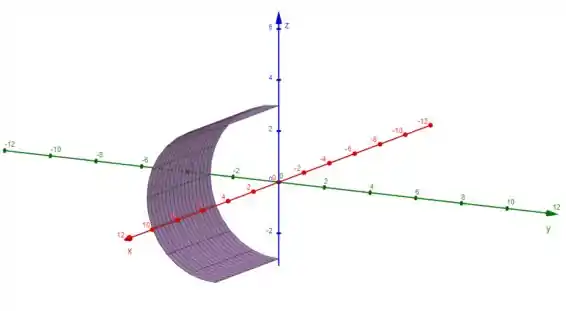
Use um sistema algébrico computacional para produzir um gráfico que se pareça com o que está dado.
Passo 1
Fala galerinha fera, tudo na paz!?
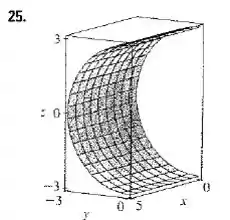
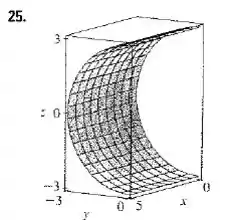
O objetivo é reproduzir um gráfico que se pareça com a figura a seguir:
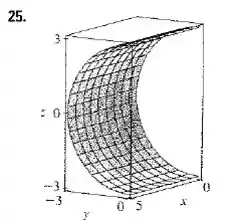
Utilize um software para fazer a representação.
Vamos pensar juntos!
Analise a figura com calma, e perceba que ela lembra muito uma porção de cilindro né.
Veja que temos um arco de círculo no plano , e conseguimos dizer também que o raio é igual a .
Sabemos que a equação de um círculo é:
Com as parametrizações:
Mas como temos um cilindro, logo vamos ter a componente variando:
Onde, pode assumir valores do eixo .
Sabendo dessas informações, você já consegue achar uma parametrização para o gráfico da figura.
Depois que você achar essa parametrização, utilize o Geogebra para plotar o gráfico. Ai faça uma comparação entre as figuras.
Vamos nessa!
Passo 2
Como vimos, temos que a equação para um círculo é:
E suas parametrizações são:
Observando a figura, podemos assumir que o raio vale , que são exatamente os extremos no eixo .
Assim, a equação fica:
Mas como temos a figura variando no eixo , podemos assumir que é uma porção de cilindro.
Logo, para representar graficamente a superfície, podemos usar equações paramétricas do tipo:
com o parâmetro no domínio:
Perceba que assumimos os ângulos variando de graus, para ficarmos com um gráfico exatamente no formato da imagem.
Passo 3
Agora que temos as parametrizações de um cilindro:
com o parâmetro no domínio:
Vamos plotar no Geogebra essa região, e verificar se realmente ela representa a figura inicial. Plotando ficamos com:
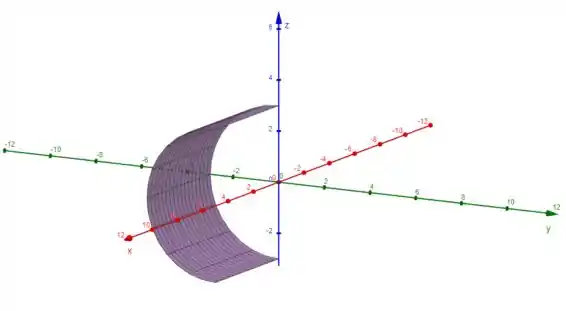
Repare que o gráfico é exatamente igual ao da figura do enunciado:
Caso queira plotar no Geogebra, pode usar o seguinte input:
a=Superfície(u,3 cos(v),3 sen(v),u,0,5,v,((π)/(2)),((3 π)/(2)))
Resposta
