Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 54
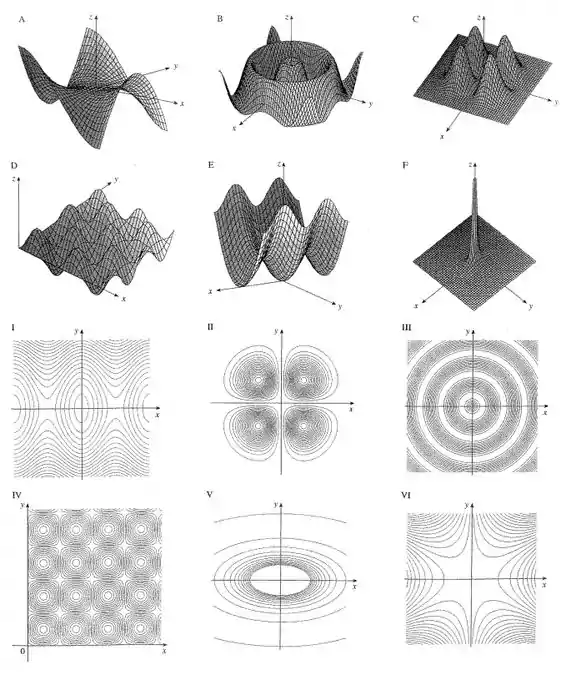
Case a função com seu gráfico (indicado por na página 899) e com seus mapas de contorno (indicado por ). Dê razões para sua escolha.
Passo 1
Fala ai rapaziada! Vamos resolver essa questão?
Nosso objetivo é analisar e representar graficamente a função usando tanto os gráficos tridimensionais quanto os mapas de contorno disponíveis. Isso permite visualizar como a função varia no espaço tridimensional e nos planos bidimensionais, respectivamente.
Como podemos fazer isso?
- Vamos entender como a equação funciona com os termos quadrático e a exponencial.
- Análise de cada gráfico.
- Verificar os mapas de contorno e interpreta-los.
Vamos começar!
Passo 2
Página 899 do livro:
Passo 3
Esta função combina um termo quadrático em e com um fator exponencial que modula a amplitude da função. Ela tem simetria em relação aos eixos e devido ao termo , mas é influenciada pela função exponencial , que controla a altura e a amplitude da superfície.
Note que se alterarmos com a função não mudará, isso nos diz que a função é simétrica nos dois eixos do plano cartesiano , além de que se aplicarmos o ponto na função nós teremos:
Sem contar que por conter a somatória de funções quadráticas temos que a função nunca poderá ser negativa.
E além desses fatos todos a função nos remete a distribuição gaussiana com cara de:
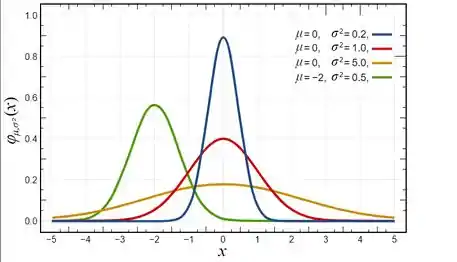
Logo teremos o gráfico cuja curva de nível bate com
