Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 56
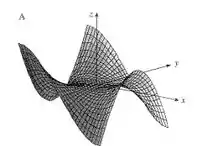
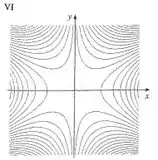
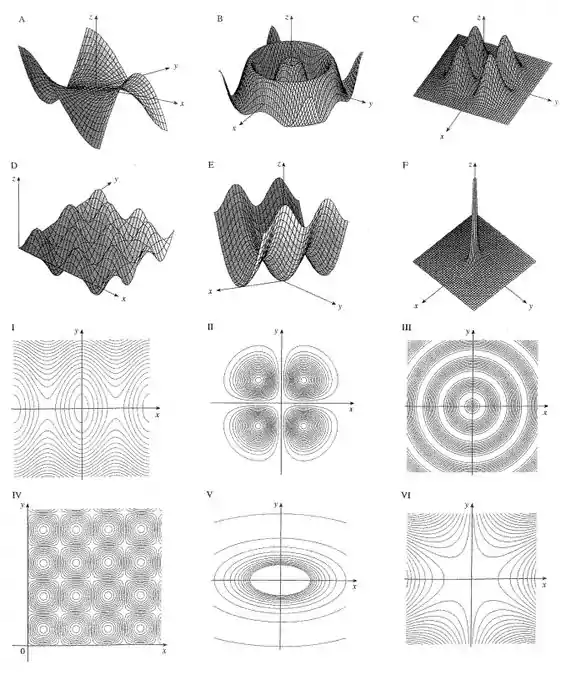
Case a função com seu gráfico (indicado por na página 899) e com seus mapas de contorno (indicado por ). Dê razões para sua escolha.
Passo 1
Olá, meu amigo. Vou te ajudar a entender e a resolver essa atividade.
A gente tem a função:
E deveremos relacionar o gráfico dessa função e a sua superfície de nível, mas para isso deveremos realizar algumas análises sobre a função, seu comportamento, pontos importantes, seu domínio e imagem.
Nessa função, iremos analisar o seu comportamento em alguns pontos, como o que acontece na origem e o que acontece no eixo .
Passo 2
A função não é limitada em (se fosse função seno e cosseno que limitariam em a ) logo pode ir sem problemas de a além de que na origem temos:
Logo também começa em .
Além de que podemos traçar funções para quando de modo que tenhamos as seguintes retas:
Para diferente de zero:
Logo temos duas retas que ditam o comportamento do gráfico.
Fazendo com que o gráfico fique entre essas retas.
O único gráfico que bate com essas características é a da letra . E a curva de nível que respeita esse gráfico é a de número romano igual a
Note que as linhas de criam assíntotas nessas duas retas diagonais.
