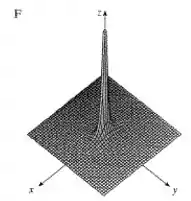
Case a função com seu gráfico (indicado por na página 899) e com seus mapas de contorno (indicado por ). Dê razões para sua escolha.
Passo 1
Fala ai rapaziada! Vamos resolver essa questão?
Nosso objetivo é analisar e representar graficamente a função usando tanto os gráficos tridimensionais quanto os mapas de contorno disponíveis. Isso permite visualizar como a função varia no espaço tridimensional e nos planos bidimensionais, respectivamente.
Como podemos fazer isso?
- Vamos entender como a equação funciona com os termos quadrático e a exponencial.
- Análise de cada gráfico.
- Verificar os mapas de contorno e interpreta-los.
Vamos começar!
Passo 2
Página :
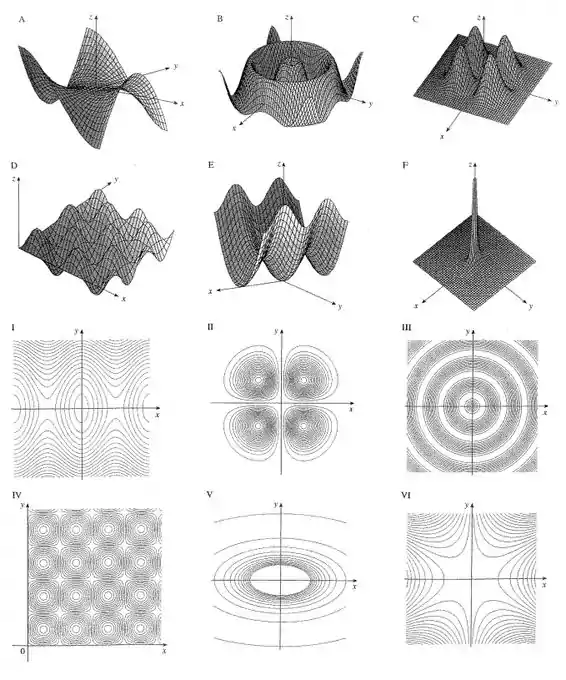
Passo 3
Vamos analisar a forma da superfície.
- A superfície é definida pela equação
- Esta função tem a forma de uma superfície hiperbólica de revolução em torno do eixo .
- A forma da superfície varia de acordo com os valores de e . Em particular, no denominador determina a altura em diferentes pontos do plano .
Simetria e comportamento.
- A função possui uma simetria em relação ao eixo devido ao termo no denominador.
- A altura aumenta confirma nos aproximamos do eixo e diminuiu à medida que nos afastamos.
Os mapas de contorno são usados para representar graficamente as curvas de nível da função . Cada curva de nível representa uma linha onde é uma constante.
- As curvas serão hipérboles equiláteras no plano
- Elas são definidas pela equação , onde é uma constante positiva.
Passo 4
Vamos analisar matematicamente.
Quando nós teremos ao seguinte comportamento da função.
O que tende a infinito e valores muito altos de e faz com que a função tenda a um comportamento igual a
O que faz tender a zero e que por e estarem em funções quadráticas e faça com que nunca seja negativa.
Então é normal imaginar que a função tenha um bico em e tenda a ter uma assíntota no plano isso é nunca poderá ser igual a zero e também nunca terá valores negativos, logo o único gráfico que bate com essa característica é com a única curva de nível sendo .