Use um computador para traçar o gráfico da função utilizando vários pontos de vista. Imprima a que, em sua opinião, saiu melhor. Se seu programa também produz curvas de nível, trace o diagrama de contornos da mesma função e compare.
Passo 1
Fala pessoal. De boa? Essa questão temos apenas que construir um gráfico com ajuda de um software. Mas que tal analisarmos um pouco para entendermos a função?
Boa ideia, né!
Vamos primeiro definir a função, gerar uma grade de pontos através do software, e por fim construir um gráfico da superfície e das curvas de nível.
Passo 2
A função seno é periódica e oscila entre e . Isso significa que, independentemente dos valores de e , o valor de sempre estará entre e .
Já o termo decresce exponencialmente à medida que aumenta. Isso significa que para grandes valores de , o argumento do seno se aproxima de zero, fazendo com que a função seno também se aproxime de zero.
Para valores negativos de , cresce exponencialmente, aumentando rapidamente o argumento do seno.
Passo 3
Vamos analisar o comportamento
- Para , , independentemente de .
- Para , pode variar rapidamente devido ao crescimento exponencial do argumento .
Passo 4
E o gráfico, como você espera que fique?
Um gráfico 3D da função mostrará uma superfície ondulada que se achata conforme aumenta. E as curvas de nível da função mostram linhas onde a função assume valores constantes.
Passo 5
Vamos montar o gráfico?
Gráfico no Geogebra:

Passo 6
Curvas de Nível:
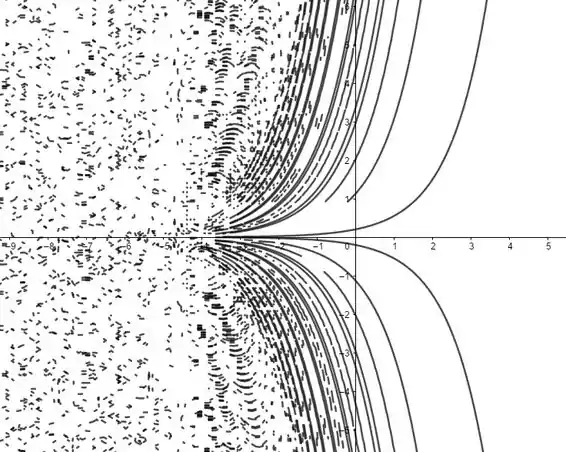
Resposta
Gráficos dos passos acima.