Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 63
Descreva como o gráfico de é obtido a partir do gráfico de
63-
Passo 1
E aí, pessoal. Tudo bem? Vamos resolver mais uma questão!
Nessa questão nós queremos responder como obter o gráfico de uma fun��ão a partir de uma outra função conhecida, .
Assim, em cada um dos casos nós vamos analisar o seguinte: conhecemos a função . Qual será a nova função como resultado de uma operação de soma ou multiplicação que fazemos na função ?
Vem comigo que eu te explico...
Passo 2
Dá para se fazer um paralelo com funções de uma variável, porém precisamos der a noção que a função e a função estão no eixo .
Na letra ()a função tem o mesmo comportamento da função só que acrescida de 2 unidades no eixo :
O paralelo em uma variável é como se fossemos chamar a função de e a função chamaremos de , tal como na figura abaixo:
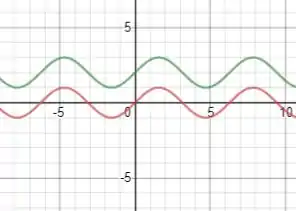
onde é a curva verde, acrescida de 2 unidades no eixo e a curva vermelha .
No caso de duas variáveis, o raciocínio da letra é o mesmo só que no eixo , ok?
Passo 3
Na letra nós esticaremos a função na vertical em duas vezes para formar o gráfico de :
Assim, no caso da função seno, vamos ter o aumento de sua amplitude em duas vezes. Formando o gráfico abaixo em uma variável.
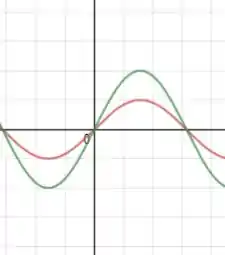
onde continuaria sendo a curva verde e vermelho a curva da função . E lembrando que para funções duas variáveis o resultado estará no eixo e não em como desenhado acima.
Passo 4
Para a letra temos que a função será o reflexo de no plano , pois onde é positivo em será negativo e vice-versa:
Em uma variável, temos que fica refletido em pelo eixo . Já em duas variáveis, todo o plano horizontal será o parâmetro para mudança de sinal, pois é o limite de mudança de sinal do eixo .
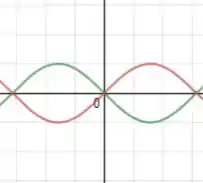
O gráfico acima ilustra uma situação em uma variável: em verde teríamos a função , enquanto em vermelho teríamos a função .
Passo 5
A letra é uma mistura braba das outras três letras (porém com uma novidade), por isso vamos por partes em relação a ela.
A novidade se dará com o termo que possui .
Mas isso não será tão novidade assim, pois já que fizemos a análise em de todas as transformações.
Se quisermos escrever a função duas unidades para cima no eixo z nós escrevemos , mas e se quisermos movimentar essa função duas unidades nos eixos e o que fazemos? Como estamos representando a função em termos de e nós podemos simplesmente fazer.
Duas unidades em :
Duas unidades em :
Isso pode ser mais simples de ver pela função visto a baixo.
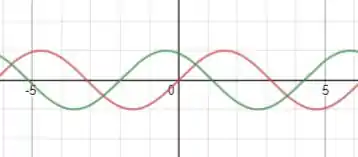
Onde agora o primeiro zero da função está em sendo transladado para a esquerda.
Então a função está transladada de 2 unidades no eixo na letra (
Passo 6
Fora isso nós invertemos o sinal da função e e depois acrescida de duas unidades no eixo , como se estivesse a seguinte representação no eixo .
