Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 58
Case a função com seu gráfico (indicado por na página 899) e com seus mapas de contorno (indicado por ). Dê razões para sua escolha.
Passo 1
Fala ai. Preparado para resolver uma questãozinha?
Vamos iniciar identificando as características da função acima. A través das características comparar os gráficos , é preciso comparar os mapas de contorno também e por fim, concluir com a correspondência.
Partiu resolver!
Passo 2
Gráfico da curva página 899
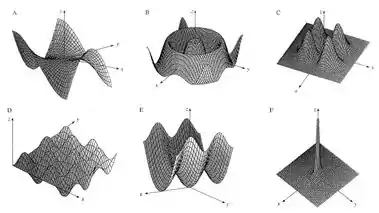
Mapa de contorno da página 899
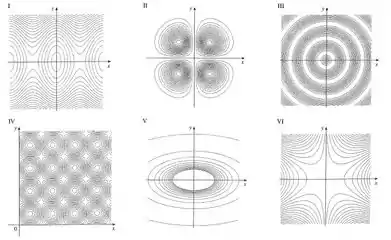
Passo 3
A função possui um gráfico que mostra ondulações periódicas no eixo , refletindo a oscilação do entre e , e uma elevação parabólica ao longo do eixo , devido ao termo .
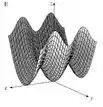
O mapa de contorno dessa função exibe elipses alongadas, indicando a combinação de oscilações no 𝑥x e crescimento quadrático em .
As linhas de nível mais próximas no mapa de contorno indicam mudanças rápidas na função, enquanto as mais espaçadas refletem variações mais suaves.
O único gráfico que bate com essas características é a de letra cuja curva de nível estará em .