Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 14
Determine e faça o esboço do domínio da função.
Passo 1
Fala ai galerinha! Tranquilo?
Vamos começar a resolver esta questão, mas antes ... Porque não entendemos um pouco do que se trata e como faremos isso!?
Para resolver a questão, vamos identificar onde a função está indefinida, vamos verificar quando o denominador é zero. A partir será possível determinarmos o domínio da função no plano.
Vamos começar!
Passo 2
Para determinamos o domínio de , queremos saber que valores de , que podem ser usados para que seja real.
Para definir o domínio é melhor olharmos para as restrições da função.
Essa função é definida somente se
Ou até mesmo se
Assim, o domínio de é
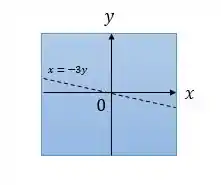
Agora, vamos esboçar o domínio da função. O domínio inclui todos os pontos do planoexceto os pontos que estão na linha .
Passo 3
Vamos desenhar no plano cartesiano?
Traçando uma linha no gráfico que represente . Esta é uma linha reta que passa pela origem e tem inclinação negativa. Vamos indicar todos os pontos do plano exceto aqueles na linha pertencem ao domínio da função.
