Uma viga com de comprimento está apoiada em uma parede e o seu topo está se deslocando para baixo a uma velocidade de . Qual será a taxa de variação de medida do ângulo formado pela viga e pelo chão quando o topo da viga estiver a do chão.
Passo 1
É bom a gente sempre tentar desenhar o que o problema está descrevendo para entender melhor!
Na diagonal, nós temos uma viga de , que forma um triângulo retângulo com a parede e o chão, como mostrado no desenho abaixo!
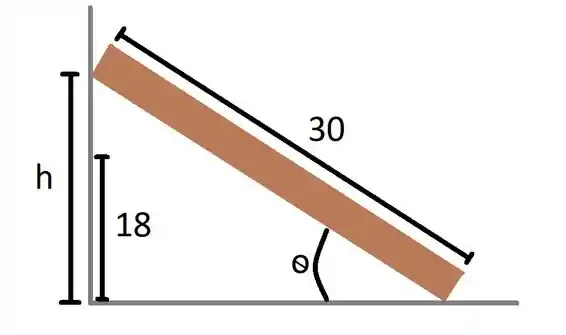
Agora que a gente visualizou o problema, vamos pensar no que temos que fazer!
O enunciado diz que a altura diminui a uma taxa de e pede a velocidade com que o ângulo diminui quando a viga estiver com a ponta que está encostada na parede a uma altura de .
Aqui nós vamos precisar utilizar nossos conhecimentos de trigonometria para relacionar as duas taxas.
Passo 2
Vamos começar tentando encontrar a relação das duas taxas. Para isso, vamos desenhar o nosso triângulo.
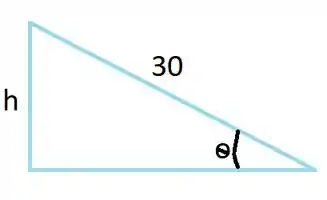
Como temos a hipotenusa, o cateto oposto e sua variação, e queremos a variação do ângulo, uma boa relação que podemos usar é a do seno,
Lembrando que tanto o ângulo como a altura variam de acordo com o tempo. Então vamos encontrar suas derivadas em função do tempo.
Passo 3
A gente pode escrever a equação da seguinte forma,
Derivando implicitamente em relação a , temos:
O problema pede a taxa de variação de medida do ângulo formado pela viga e pelo chão quando o topo da viga estiver a do chão. Então agora vamos encontrar o valor de nesse ponto, antes de substituir tudo nessa equação que acabamos de encontrar.
Passo 4
A gente consegue achar o valor de , substituindo na equação do seno, onde o cateto oposto será e a hipotenusa (se não ficou claro, da uma olhada no nosso primeiro desenho).
Passo 5
Agora sim, vamos substituir os valores na equação que encontramos no . Temos que,
Substituindo os valores:
Como as unidades estavam em metros e segundos a resposta será dada em radianos por segundo
Ufaaa, pronto terminou, espero ter ajudado :3