Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 29
Uma cidade medieval tem a forma de um quadrado e é protegida por muralhas com comprimento de e altura de . Você é o comandante de um exército atacante e o mais próximo que pode chegar da muralha é . Seu plano é incendiar a cidade arremessando com catapultas rochas aquecidas sobre a muralha (com velocidade escalar inicial de ). Em que intervalo de ângulos você deve dizer a seus homens para armar a catapulta? (Suponha que a trajetória das rochas seja perpendicular à muralha).
Passo 1
Olá, tudo bem? Para resolver essa questão vamos fazer um desenho e pegar todas as informações que o enunciado trás.
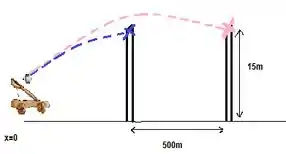
A catapulta está a atrás da primeira muralha e a uma distância de da segunda muralha.
A altura que a rocha deve atingir é o topo da muralha (que tem de altura), tanto na muralha mais próxima, quanto na muralha mais distante.
Sendo assim, devemos encontrar uma equação para o alcance de cada muralha.
As posições das muralhas são e .
Queremos calcular o intervalo de ângulos que deveremos armar a catapulta.
Para isso, deveremos utilizar a equação da posição em função do tempo :
Onde é a componente horizontal da velocidade, é a altura, é a componente vertical da velocidade e é a aceleração da gravidade.
Passo 2
Aplicando as componentes da velocidade para colocarmos o ângulo de disparo, temos:
Para a muralha mais próxima, a componente horizontal do vetor posição nos dá o tempo que a rocha leva para chegar até a posição horizontal de .
Resgatando a componente horizontal, temos:
Agora é só substituir esse valor de na componente vertical da posição e assim ter uma expressão apenas em , sacou? Bora lá? Admitindo que a catapulta está na origem das posições, a componente vertical da posição é:
Agora substituindo o valor de temos:
Passo 3
Vamos arrumar um pouco essa expressão pra ficar mais simpática:
Agora vamos lembrar da identidade trigonométrica e substituir na equação ali em cima:
Dividindo toda a equação por ficamos:
Uma equação de segundo grau em . Parece estranha, mas vamos trocar por , daí você vai achar mais tranquilo (não faz sentido, eu sei, mas funciona kkk):
Viu, agora não assusta tanto, não é? Pela fórmula de bháskara:
Como , temos dois valores a serem considerados:
Então a variação de
Passo 4
Para a muralha mais distante, a componente horizontal do vetor posição nos dá o tempo que a rocha leva para chegar até a posição horizontal de .
Resgatando ali do passo a componente horizontal temos:
Agora é só substituir esse valor de na componente vertical da posição e assim ter uma expressão apenas em , sacou? Bora lá? Admitindo que a catapulta está na origem das posições, a componente vertical da posição é:
Agora substituindo o valor de temos:
Passo 5
Vamos arrumar um pouco essa expressão pra ficar mais simpática:
Agora vamos lembrar da identidade trigonométrica e substituir na equação ali em cima:
Dividindo toda a equação por ficamos:
Uma equação de segundo grau em . Parece estranha, mas vamos trocar por , daí você vai achar mais tranquilo (não faz sentido, eu sei, mas funciona kkk):
Viu, agora não assusta tanto, não é? Pela fórmula de bháskara:
Como , temos dois valores a serem considerados:
Então a variação de