Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 22

Um cilindro circular reto está inscrito num cone circular reto de altura H = 6   m e raio da base R = 3,5   m . Determinar a altura e o raio da base do cilindro de volume máximo.

Passo 1

Inicialmente, vamos fazer um esboço do que está acontecendo, olha só:

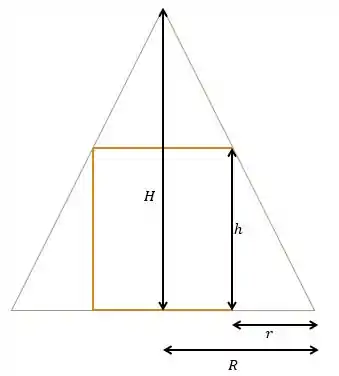
Repare que o triangulo retângulo pequeno, é semelhante ao triangulo retângulo grande. Assim,

h r = H R

Como H = 6   m e R = 3,5   m :

h r = 6 3,5

Logo,

h = 12 7 r

Passo 2

Para acharmos o maior cilindro, vamos expressar o volume e maximizar. Vem comigo!

V = A b a s e × h

Logo,

V = π 3,5 - r 2 h

Substituindo a expressão de h que encontramos no Passo 1:

V = π 3,5 - r 2 12 7 r

Assim,

V ' r = 12 7 3,5 - r 2 r

Para maximizar, vamos derivar a expressão de V e igualar a zero. Usando a regra do produto:

V ' r = 12 7 2 3,5 - r × - 1 × r + 3,5 - r 2

Igualando a zero:

12 7 2 3,5 - r × - 1 × r + 3,5 - r 2 = 0

Simplificando, temos:

3,5 - r 2 = 2 r 3,5 - r

Como r ≠ 3,5 :

3,5 - r = 2 r

Logo,

r = 3,5 3 → r = 7 6   m

Passo 3

Voltando na ilustração do Passo 2, vemos que o raio da base do cilindro é dado por:

r b a s e = R - r

Assim,

r b a s e = 7 2 - 7 6

Fazendo as contas:

r b a s e = 7 3

E pela relação do Passo 1, vemos que a altura do cilindro é dada por:

h = 12 7 r

Logo,

h = 12 7 × 7 6 → h = 2   m

Resposta

r = 7 3   m

h = 2   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Responda às perguntas seguintes sobre as funções cujas derivadas são dadas:Quais são os pontos críticosEm quais intervalos f é crescente ou decrescente?Em quais pontos, se houver f assume máximos e mí
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem f θ = 6
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem h x =2 x
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem k t = 15
Determine os intervalos abertos em que a função é crescente e aqueles em que ela é decrescenteIdentifique os valores extremos absolutos e locais das funções, se houver, indicando onde ocorrem h r = r