Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 10

Qual é o retângulo de perímetro máximo inscrito no círculo de raio 12   c m ?

Passo 1

Inicialmente, podemos fazer uma ilustração para entender melhor o que está acontecendo. Assim,

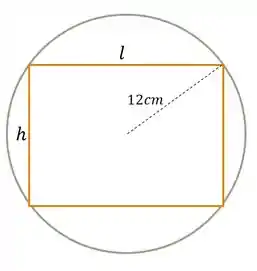
Como o raio da circunferência é 12   c m , então a diagonal do retângulo será 24   c m . Para relacionar l e h , podemos fazer o teorema de Pitágoras.

l 2 + h 2 = 24 2

Isolando o h :

h = 24 2 - l 2     i

Passo 2

Como queremos saber a valor máximo do perímetro, vamos começar montando uma expressão para ele. Chamando o perímetro de y :

y = 2 l + 2 h

Da expressão ( i ) :

y = 2 l + 2 24 2 - l 2

Para achar o perímetro mínimo, vamos derivar. Assim,

y ' = 2 + 2 1 2 × 1 24 2 - l 2 × 24 2 - l 2 '

Cuidado para não esquecer da regra da cadeia.

y ' = 2 - 2 l 24 2 - l 2

Passo 3

Para acharmos os pontos critico, vamos igualar a zero. Assim,

2 - 2 l 24 2 - l 2 = 0

Portanto,

2 24 2 - l 2 = 2 l

Simplificando:

24 2 - l 2 = l

Elevando os dois lados ao quadrado:

24 2 - l 2 = l 2

Logo,

l 2 = 24 2 2 → l = 288

Para acharmos h , basta usarmos a relação do Passo 1:

h = 24 2 - l 2  

Assim,

h = 24 2 - 288

portanto,

h = 288

Como encontramos l = h = 288 , teremos um quadrado de lado 288 .

Resposta

Quadrado de lado 288

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determina os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. f
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. f
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos exemplos 3 e 4 dessa seção. Faça um esboço do gráfico da função no intervalo. f x = x
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos exemplos 3 e 4 dessa seção. Faça um esboço do gráfico da função no intervalo. f x = x
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. f