Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 39
Um arame de cm de comprimento deve ser cortado em dois pedaços, um dos quais será torcido de modo a formar um quadrado e o outro, a formar uma circunferência. De que modo deverá ser cortado para que a soma das áreas das regiões limitadas pelas figuras obtidas seja mínima?
Passo 1
O enunciado nos diz que o arame tem , ele é cortado em dois pedaços que vamos chamar de e . Assim temos:
Vamos dizer que o lado do quadrado é igual a , então:
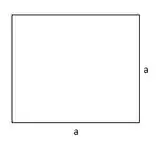
Já a circunferência tem perímetro igual a e raio igual a :
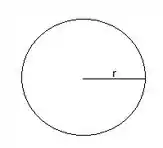
Passo 2
Como queremos que a soma das áreas das regiões limitadas pelas figuras seja mínima vamos somar as áreas, e substituir os valores de e que encontramos em cima:
Vamos então isolar o da expressão do dos segmentos e substituir na fórmula da área:
Substituindo:
Fazendo o m.m.c. temos:
Vamos dar uma arrumadinha:
Passo 3
Aqui temos uma função quadrática, onde:
Lembrando que esse aqui é o coeficiente do polinômio e não o lado do quadrado.
Como então a nossa função tem a concavidade pra cima. Lembra que a gente quer a área mínima?Exatamente! O vértice da função!
Vamos calcular e depois substituir em :
Opa, achamos o comprimento do primeiro pedaço, agora vamos para o segundo:
Temos então que os segmentos são e .
Resposta
e