Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.8 - Ex. 16
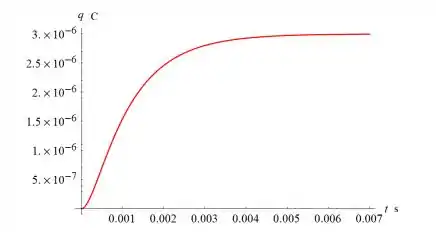
Um circuito em série tem um capacitor de 0,25 × 10^–6 F, um resistor de 5 × 10³ Ω e um indutor de 1 H. A carga inicial no capacitor é zero. Se uma bateria de 12 volts for conectada ao circuito e o circuito for fechado em t = 0, determine a carga no capacitor em t = 0,001 s, em t = 0,01 s e em qualquer instante t. Determine, também, a carga limite quando t → ∞.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a solução da nossa equação. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser relembrar que temos o seguinte:
Passo 3
Pronto!! Agora é só substituir os valores e achar a solução!!
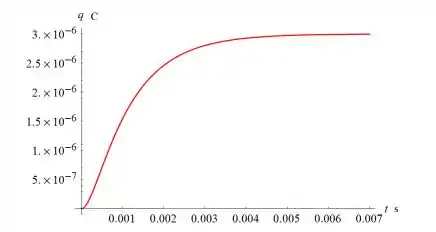
Resposta
Exercícios de Livros Relacionados
No problema 3, determine a equação do movimento se a força externa for f t = e - t . s e n ( 4 t ) . Analise o deslocamento quando t → ∞ .
Uma massa de 0,5 kg é atada a uma mola que tem constante de elasticidade igual a 6 N/m. A massa parte do repouso 2 m abaixo da posição de equilíbrio e o movimento subsequente está sujeito a uma força
Resolva a equação diferencial do problema precedente se a mola distende-se 4 cm com um peso de 0,5 kg, e β = 2 , h t = 5 . c o s ( t ) , x 0 = x ' 0 = 0
Uma massa de 1 kg é atada a uma mola cuja constante vale 5 N/m. A massa é solta 1 cm abaixo da posição de equilíbrio com uma velocidade de 5 cm/s para baixo. O movimento subsequente tem lugar em um me
Compare o resultado obtido na parte (b) do problema 15 com a solução obtida usando variação dos parâmetros quando a força externa for F 0 . c o s ( ω t )