Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.9 - Ex. 29
Dois lados de um triângulo são e , o ângulo entre eles está crescendo a uma taxa de rad/s. Encontre a taxa segundo a qual a área está crescendo quando o ângulo entre os lados de comprimente fixo for .
Passo 1
Opa, bora resolver esse problema! Temos um triângulo com as seguinte medidas:
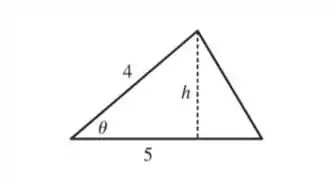
Onde , é o ângulo descrito entre os lados fixos e , a altura do triângulo. Aqui esta crescendo a uma taxa de:
Queremos:
Quando o ângulo entre os lados de comprimente fixo for .
Passo 2
A altura em função do ângulo é:
Portanto, a área é:
Derivando em função do tempo:
Quando o ângulo é e a taxa com que ele varia é rad/s, temos:
Logo, a taxa com que a área varia é de .
Resposta
A taxa com que a área varia é de .
Exercícios de Livros Relacionados
Uma escada de 8m está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé́ da parede a uma velocidade constante de 2 (m/s), com que velocidade a extremidade superior estar
Dois pontos P e Q deslocam-se, respectivamente, nos eixos x e y de modo que a soma das distâncias de P a R e de R a Q mantém-se constante e igual a e durante o movimento, em que R = 0 , h é um ponto
Seja f t = t 3 + 3 t 2 .a) Estude o sinal de f ' t .b) Estude o sinal de f ' ' t .c) Calcule lim t → + ∞ t 3 + 3 t 2 e lim t → - ∞ t 3 + 3 t 2 .d) Utilizando as informações acima, esboce o gráfico
A equação abaixo da a posição s = f ( t ) de um corpo que se desloca em uma reta coordenada (s em metros, t em segundos). Determine a velocidade, o módulo da velocidade, a aceleração e a sobreaceleraç
A equação abaixo da a posição s = f ( t ) de um corpo que se desloca em uma reta coordenada (s em metros, t em segundos). Determine a velocidade, o módulo da velocidade, a aceleração e a sobreaceleraç