Um cocho tem de comprimento e seus extremos têm a forma de triângulos isósceles invertidos, com de altura e de base. Água está fluindo no cocho a uma taxa de . Com que velocidade estará se elevando o nível da água quando a profundidade for ?
Passo 1
As vezes o enunciado deixa a gente confuso hahaha mas relaxa que vamos tirar de letra. Caso você não saiba o que é um cocho, saber pode ajudar! Um cocho é um recipiente em que comem ou bebem bois e outros animais. Ou seja, é isso aqui:

Beleza, agora que entendemos isso, vamos ver o cocho da nossa questão:
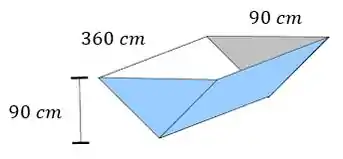
Então vamos partir daí pra modelar essa questão e resolver!
Passo 2
Bem galera, vamos imaginar que a água esteja a uma altura em relação a ponta do triângulo invertido que é o extremo do cocho. Podemos representar o nível d’água assim:
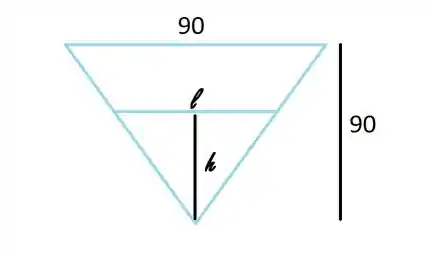
Ok, mas como isso ajuda? Bem, veja só, quando adicionamos água no cocho, a água assume o mesmo formato do cocho. Portanto o volume de água pode ser calculado pela fórmula do volume de um prisma:
Sendo o volume de água, a área do triângulo que á agua faz e o comprimento do cocho. O volume fica então:
Opa, mas o volume depende de duas variáveis? Sim, mas não por muito tempo! Esse é o momento que a gente relaciona as variáveis. Como o enunciado relaciona a taxa de volume de água com a velocidade do o nível de água, a variável que a gente não precisa é o ! Sendo assim, buscaremos:
De forma que:
Bem, se olharmos bem pra imagem, vamos ver que o triângulo da extremidade do cocho e o da água são semelhantes! Portanto:
E tá na mão:
Passo 3
Show, agora que o conceito de taxa vai ser usado. Como uma taxa é nada mais nada menos que a derivada no tempo, derivamos :
Pela regra da cadeia:
Beeleeeeza! Saca só isso: a gente sabe, do enunciado, que em determinado instante qualquer a taxa de aumento do volume de água será:
E que nesse mesmo instante, o nível de água será:
A gente pode até não saber quem é , mas com essas duas informações achamos:
E taí! Esse é o valor da taxa de variação da altura do nível de água no instante em que o nível é de , ou como o enunciado disse, a velocidade de elevação do nível de água. Com as devidas unidades de medida, temos: