Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.3 - Ex. 16
O raio de um cone é sempre igual à metade de sua altura . Determinar a taxa de variação da área da base em relação ao volume do cone.
Passo 1
Vamos para mais uma questão de taxa de variação, galerinha! Queremos achar a taxa de variação da área da base em relação ao volume do cone. Bem, vamos dar uma olhada no cone:
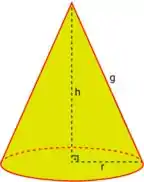
Como todo bom cone, seu volume é:
Vamos partir daqui, belezinha? Afinal, temos que rever a expressão de pra equação acima só ser uma função da área da base () e do volume do cone ()! Ai sim poderemos derivar um em relação ao outro e achar a taxa de variação!
Passo 2
Bem pessoal, a base não é um círculo? Então a área da base vai ser:
Nesse caso em específico, o enunciado disse pra gente que:
Portanto a área será:
E a altura em função da área será:
Substituindo na expressão do volume:
Elevando os dois lados ao quadrado:
E pra achar a taxa de variação da área da base em relação ao volume do cone, basta derivar em relação a ! Partiu!
Passo 3
Sendo:
Usando regra da cadeia, temos:
Podemos arrumar essa expressão aí! Saca só:
Portanto a taxa de variação da área em relação ao volume será:
Resposta
A taxa de variação da área da base em relação ao volume do cone: