Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.6 - Ex. 32
Coloque a equação na forma padrão, classifique a superfície e esboce-a.
Passo 1
Vamos escrever da forma:
E, pronto. Essa é a equação de um paraboloide hiperboloide centrado em , com eixo central no eixo (porque o está positivo) O esboço fica:
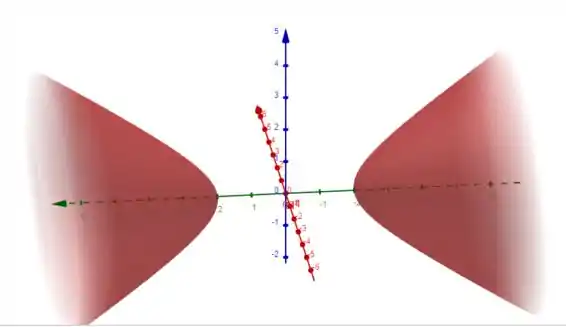
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use um computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela retangular até conseguir uma boa visão da superfície. x 2 -
Use um computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela retangular até conseguir uma boa visão da superfície. - 4 x
Coloque a equação na forma-padrão, classifique a superfície e esboce-a. 4 y 2 + z 2 - x - 16 y - 4 z + 20 = 0
Esboce a região delimitada pelos paraboloides z = x 2 + y 2 e z = 2 - x 2 - y 2 .
Determine uma equação da superfície constituída de todos os pontos P para os quais a distância de P ao eixo x é o dobro da distância de P ao plano y z . Identifique a superfície.