Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.1 - Ex. 29
Esboce o gráfico da função.
Passo 1
Fala aí! Precisamos escrever o gráfico dessa função…
A gente tem a função:
E ela é um pouco diferente das notações que você está acostumada, que são assim:
O que a gente tem aqui é uma curva em 3 dimensões, um plano para ser mais específico, onde a equação é representada da seguinte forma:
Depois que a gente representar a função daquela forma, a gente vai analisar ela para ver se ela é semelhante, ou se podemos reescrever ela de forma semelhante a uma função conhecida.
Passo 2
Bom, vamos começar reescrevendo a função desse jeitinho aqui:
Vamos modificar mais uma coisa… vamos reescrever de forma que esse fique no denominador, ok?
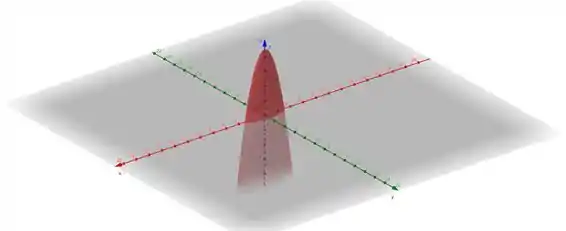
Opa! Olha só, essa é a equação de um paraboloide elíptico!
Veja que por termos ele está deslocado unidades para cima no eixo , sigficando que o sólido tem sua origem em .
Para descobrirmos os pontos de interseção com os eixos, basta que a gente zere dois eixos, e assim iremos descobrir. Veja:
Então temos onde ele toca o eixo , vamos agora ao eixo .
E observando os sinais de e de , que são negativos, vemos que ele tem a concavidade voltada para baixo, né? E observando os valores que acompanham as incógnitas… temos que o vértice dele é em … Show! Agora é desenhar isso aí… esquisito, mas a gente consegue, ok? Vai ficar assim:
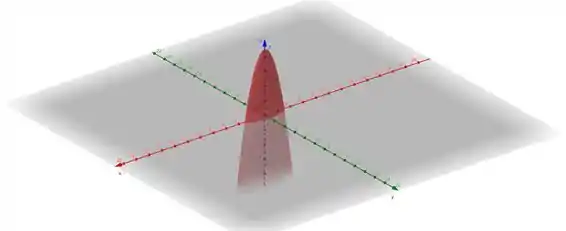
Resposta
