Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 12.6 - Ex. 29
Coloque a equação na forma-padrão, classifique a superfície e esboce-a.
Passo 1
Hey, galera! Primeiro vamos dar uma ajeitada na equação pra deixar ela na forma-padrão, ok?
Passo 2
Show! Chegamos à forma-padrão da equação do hiperboloide de duas folhas! Agora só falta esboçar:
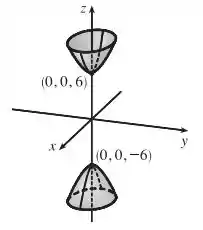
Resposta
Hiperboloide de duas folhas
Exercícios de Livros Relacionados
Determine uma equação da superfície obtida pela rotação da reta x = 3 y em torno do eixo x .
Determine uma equação da superfície constituída de todos os pontos que são equidistantes do ponto - 1 ,0 ,0 e do plano x = 1 . Identifique essa superfície.
Determine uma equação da superfície obtida pela rotação da parábola y = x 2 em torno do eixo y .
Uma torre de resfriamento de um reator nuclear deve ser construída na forma de um hiperboloide de uma folha. O diâmetro na base é 280m e o diâmetro mínimo, 500m acima do solo, é 200m . Encontre uma eq
Desenhe as superfícies z = x 2 + y 2 e z = 1 - y 2 em uma mesma tela usando uma janela de tamanho x ≤ 1,2 , y ≤ 1,2 , e observe a curva de intersecção. Mostre que a projeção dessa curva no plano x y é