Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.6 - Ex. 43
Determine uma equação da superfície obtida pela rotação da parábola em torno do eixo .
Passo 1
Beleza, galera? Se rotacionarmos uma parábola em torno do eixo , estaremos criando um paraboloide circular, veja só:
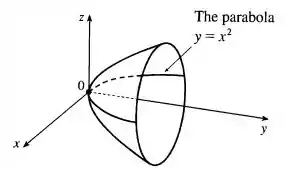
Isso faz sentido, porque se cortarmos essa superfície pelo plano ou pelo plano , obteremos parábolas.
Passo 2
Show! O vértice desse paraboloide é a origem, e ele se abre no sentido positivo do eixo , então sua equação deve ser:
Resposta
Exercícios de Livros Relacionados
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. y 2 = x 2 + z 2
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. x 2 + 4 z 2 - y = 0
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. x 2 + 4 y 2 + z 2 = 4
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. z = x 2 - y 2
Use o computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela de inspeção até conseguir uma boa visão da superfície.38- 8 x