Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 44
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Opa, tudo tranquilo? Questãozinha de coordenadas polares, vamos lá!
A questão nos dá a função
E pede para modelarmos dois gráficos: O gráfico em coordenadas cartesianas e o gráfico em coordenadas polares!
Para o gráfico em coordenadas cartesianas podemos imaginar como se a função fosse
Dessa forma, para modelar ambos os gráficos a gente pode atribuir valores para (ou ) até modelar o formato geral da função!
Passo 2
Seja a função
Ou ainda
Se quisermos modelar o gráfico em coordenadas cartesianas dessa função, primeiramente precisamos observar que ela não está definida (pelo menos no conjunto dos números reais) para
Afinal, em teríamos uma indeterminação e para teríamos sendo um número imaginário!
Dessa forma, se atribuirmos valores para nós desenhamos o seguinte gráfico
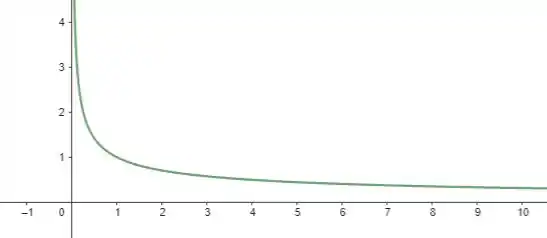
Onde a gente observa que, conforme se aproxima de , tende ao infinito! E além disso, conforme se aproxima do infinito positivo, tende a !
Passo 3
Agora queremos esboçar
Ou ainda
Lembrando: Nas equações polares o representa a distancia do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Bem similar ao caso anterior, observamos que a função só está definida para
Pois para temos uma indeterminação, e para temos imaginário!
Agora vamos analisar essa curva:
Para o intervalo , o valor de começa em um número absurdamente grande (próximo do infinito) e conforme se aproxima de , diminui;
Em o valor de é 1;
E, por fim, conforme continua aumentando, o diminui!
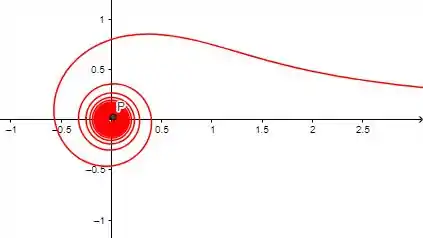
Então se a gente for atribuindo valores para no intervalo nós conseguimos desenhar o seguinte gráfico
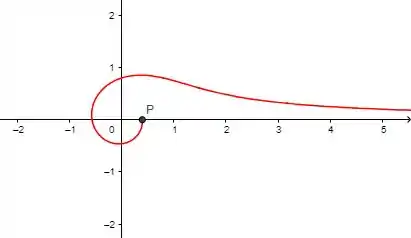
E se continuarmos atribuindo valores para , conforme aumenta a espiral continua (e continua diminuindo), de forma que
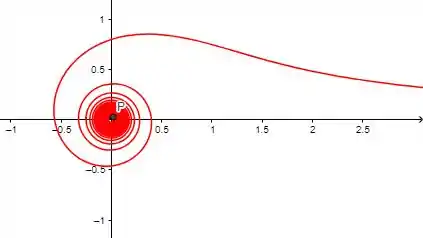
Resposta
Gráfico de em coordenadas cartesianas
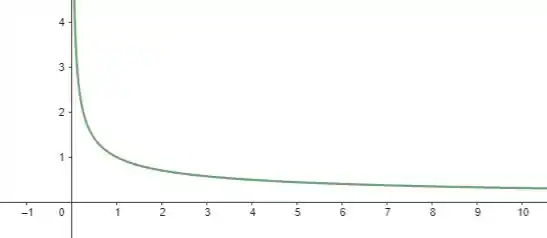
Gráfico de em coordenadas polares
