Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.3 - Ex. 2
No começo desta seção discutimos a função , onde era o humidex; , a temperatura; e , a umidade relativa. Utilize a Tabela 1 para estimar e . Quais são as interpretações práticas desses valores?
Passo 1
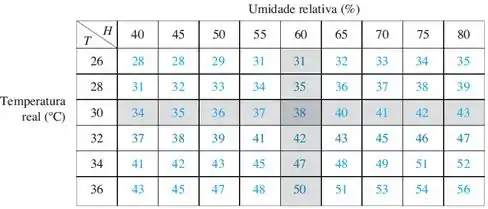
Como primeiro passo, vamos retomar a tabela com os valores da função nos pontos fornecidos:
Show de bola, galera!
A questão quer que a gente estime a derivada parcial da função no ponto
Para responder isso, precisamos ver como vamos fazer pra estimar aquelas derivadas parciais do enunciado...Partiu? 
Passo 2
Vamos fazer 2 estimativas para e , respectivamente, e usar a média dessas estimativas como estimativa final. Ficou confuso? Calma!
Aqui nós vamos usar a definição de derivada parcial.
Se temos uma função e queremos calcular a derivada de com relação a , nós temos que deixar a variável fixa e fazer pequenas variações em torno do valor de
Matemáticamente, escrevemos:
Na nossa tabela, para um valor fixo de só há dois valores possíveis de para fazermos essa variação.
Por exemplo, veja na imagem abaixo que os valores de mais próximos de são e .
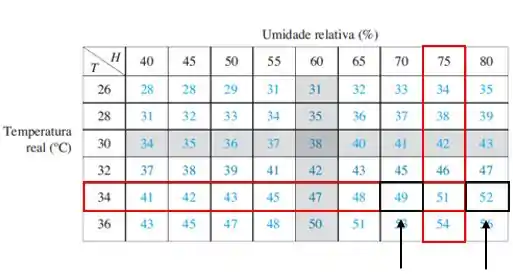
Assim, quando mantemos constante e variamos , temos os pontos e . Os valores de nesses pontos estão em preto e indicados pelas setas.
Vamos fazer a mesma sequência de passos para calcular Na imagem abaixo nós podemos ver a interseção da linha e coluna para o ponto
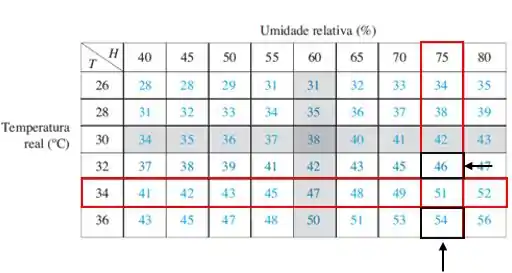
Agora fixamos e variamos Podemos ver que os pontos vizinhos ao são e e seus respectivos valores apontados em preto.
Passo 3
Vamos fazer o seguinte:
onde é a aplicação da fórmula da derivada parcial de com relação a usando como referência o primeiro ponto vizinho. Da mesma forma, é a aplicação da fórmula da derivada parcial de com relação a usando como referência o segundo ponto vizinho.
Chega de falação, vamos às contas:
Agora fazemos o mesmo procedimento, mas pensando na derivada com relação a :
Vamos às contas novamente!
Assiiimm....