Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.3 - Ex. 2
No começo desta seção discutimos a função , onde era o índice de calor; , a temperatura; e , a umidade relativa. Utilize a Tabela 1 para estimar e . Quais são as interpretações práticas desses valores?
Passo 1
Fala aí pessoal. Tranquilo?
Bora fazer uma questãozinha!
A questão nos pede para estimar e . E para isso precisaremos utilizar a definição de derivada para duas variáveis.
Devemos verificar na tabela mencionada os termos da equação e substituir.
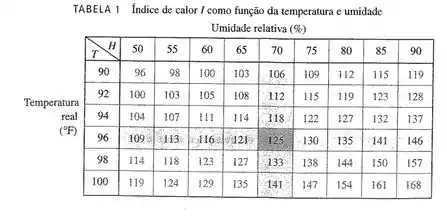
Observação importante!!! Na tabela nos dá a variação da temperatura e unidade, isso significa que teremos que escolher dois pontos (antes e depois do ponto dado) para calcular e no final verificar a média pela equação.
No final teremos a resposta! 😉
Vamos começar!
Passo 2
Vamos encontrar . Vamos nos atentar que a tabela, varia de em , Logo
Substituindo, temos (depois).
Substituindo.
Agora (antes)
Substituindo.
Logo a variação instantânea da umidade será igual a:
Passo 3
Vamos encontrar . Vamos nos atentar que a tabela, varia de em. Podemos então verificar a é a variação do ponto atual para o ponto antes da tabela e é a variação do ponto atual para o ponto depois da tabela
Substituindo, temos (depois).
Substituindo, temos (antes).
Logo a variação instantânea da temperatura será:
De forma prática esses valores significam que no instante que o índice de calor está em a temperatura estará aumentando a uma taxa de e quando a umidade está em a umidade estará aumentando a uma taxa de