Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 67

Um cometa move-se numa órbita parabólica em torno do Sol que está no foco F da parábola. É feita uma observação quando ele está num ponto P1, a 15 milhões de quilômetros do Sol e uma segunda quando ele está em P2, a 5 milhões de quilômetros do Sol. Os segmentos de reta FP1 e FP2 são perpendiculares. Com essas informações, existem duas órbitas possíveis para o cometa. Ache qual a menor distancia ao sol para cada Órbita.

Passo 1

Essa questão precisa de um pouco mais de atenção que o normal. Vamos com calma galera.

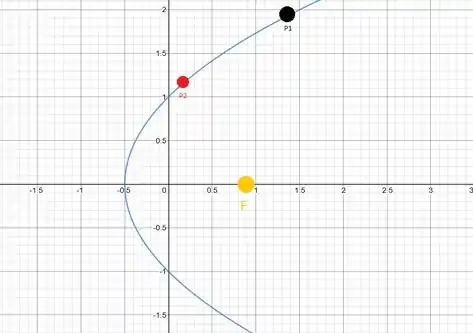
Primeiros temos as distancias do Foco (sol) ate as posições dos cometas (P1 e P2), ou seja, ele nos da o modulo do vetor FP1 e vetor FP2.

F P 1 = 15

F P 2 = 5

Também sabemos que uma equação de uma parábola é de:

y 2 = 4 p x

Então para cada vetor, temos que:

y 1 2 = 4 p x 1

y 2 2 = 4 p x 2

Desenvolvendo a equação das distancias:

F P 1 = 15

x 1 , y 1 - p , 0 = 15

x 1 - p , y 1 = 15

( x 1 - p ) 2 + y 1 2 =   15

x 1 = 15 - p (1)

Para o FP2 é o mesmo desenvolvimento, logo:

x 2 = 5 - p (2)

Passo 2

Então para acharmos a menor distancia, precisamos fazer o produto vetorial dos nossos dois vetores e igualar a 0, para achar a nossa equação mínima... SIMBORA!

F P 1 → * F P 2 → = 0

( x 1 - p , y 1 ) *   ( x 2 - p , y 2 ) = 0

Aplicando as nossas equações (1) e (2):

( 15 - 2 p , 4 p 15 - p   ) * ( 5 - 2 p , 15 - 2 p , 4 p 5 - p ) = 0

Fazendo os produtos temos que:

75 - 30 p - 10 p + 4 p 2 + 4 p ( 75 - 15 p - 5 p + p 2 = 0

75 - 40 p + 4 p 2 + 4 p ( 75 - 20 p + p 2 = 0

Passo 3

Agora temos que resolver essa equação gigante para acharmos a menor distância.

75 - 40 p + 4 p 2 + 4 p ( 75 - 20 p + p 2 = 0

Resolvendo, temos que as raízes da equação são:

3 ± 3 4 6   m i l h õ e s   d e   k i l o m e t r o s

Resposta

3 ± 3 4 6   m i l h õ e s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 23 e 24, ache um conjunto de coordenadas polares dos pontos cujas coordenadas cartesianas retangulares são dadas. Tome r0 e 0 ≤ θ ≤ 2 π .24(b) ( - 1 ,3 )
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas22(c) ( 2 ,- 7 6 π )
Nos exercícios de 25 a 34, ache a equação polar do gráfico dada a sua equação cartesiana.25. x 2 + y 2 = a 2
Nos exercícios 23 e 24, ache um conjunto de coordenadas polares dos pontos cujas coordenadas cartesianas retangulares são dadas. Tome r0 e 0 ≤ θ ≤ 2 π .23(a) ( 1 ,- 1 )
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas22(b) ( - 1 ,1 4 π )