Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 46
Compare as funções e traçando os gráficos de e em várias janelas retangulares. Quando finalmente o gráfico de ultrapassa o de ?
Passo 1
E aeee, belezinha??
Bom, primeiro o exercício pede que a gente trace o gráfico dessas funções em diferentes “regiões” do plano coordenado.
Assim, vai ser possível dizer quando que ultrapassa a .
E aí? Bora lá??
Passo 2
Vamos pegar primeiramente uma janela e :
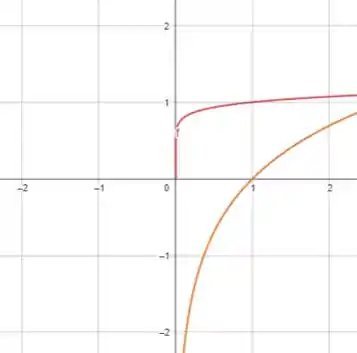
Aqui, vemos que as funções ainda não se encontraram e que não precisamos aumentar a janela em , apenas em .
Ademais, como não existem valores negativos de para as duas funções, podemos partir da origem.
Passo 3
Fazendo agora para e :
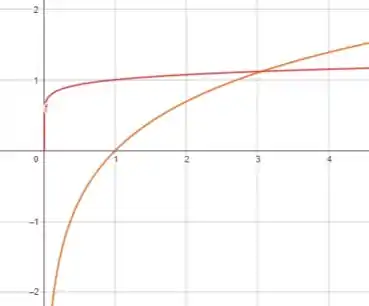
Aqui já vemos o ponto em que as curvas se tocam (algo próximo de ), que é o ponto que ultrapassa o de .
Para descobrir seu valor em , basta substituir em qualquer uma das duas funções:
Assim, trata-se do ponto .