Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 48
Faça o esboço do gráfico de cada função. Não use a calculadora. Use somente os gráficos dados nas Figuras 12 e 13 e, se necessário, as transformações da Seção 1.3.
- (b)
Passo 1
Primeiro, as figuras citadas não enunciado são as seguintes:
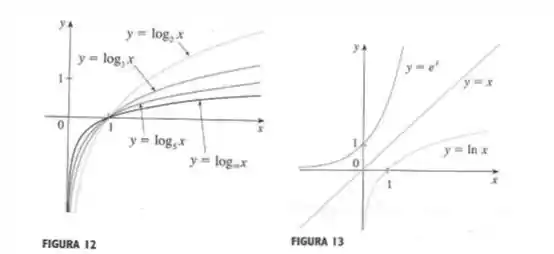
E as transformações da Seção 1.3 são:
(deslocamento do gráfico para cima)
(deslocamento do gráfico para baixo)
(deslocamento do gráfico para a direita)
(deslocamento do gráfico para a esquerda)
Belexa, então, tendo isso em mente, temos que esboçar os gráficos das funções e
Passo 2
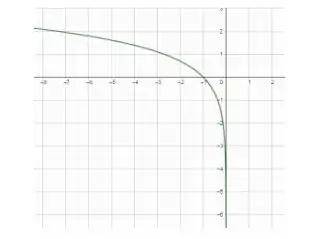
Para (a), sabemos, pela figura 12, como é o gráfico de :
Aqui, podemos ver que o só existe para valores positivos, certo?
Como queremos , tem que ser positivo. Isso só acontece quando é negativo. No gráfico, o que acontece é a reflexão em torno do eixo :
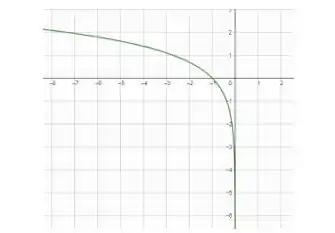
Beleza, temos o gráfico de
Passo 3
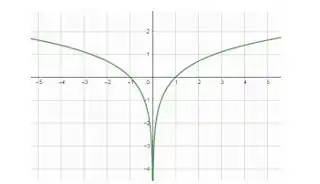
Para (b), temos que achar .
Como vimos no passo anterior, a função do logaritmo natural só pode assumir valores positivos. Aqui, estamos usando o módulo, então não teremos problemas com isso: valores negativos de também assumirão valores de . Vamos juntar os gráficos de e :
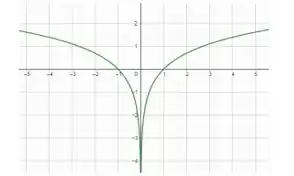
Pronto!
Resposta
