Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.Exercícios práticos - Ex. 80

Compare as precisões das aproximações s e n   x   ≈   x e s e n   x   ≈   6 x / ( 6   +   x ² ) comparando os gráficos de f   ( x )   =   s e n   x   -   x e g ( x )   =   s e n   x   -   ( 6 x / ( 6   +   x ² ) ) . Descreva o que você encontrar.

Passo 1

Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?

Sabemos que a série de potência para s e n   x é dada por:

s e n   x = x - x 3 3 ! + x 5 5 ! - …

Observe que s e n   x   ≈   x é uma aproximação linear e s e n   x   ≈ 6 x 6   +   x 2 é a aproximação quadrática de s e n   x . Portanto, teoricamente s e n   x   ≈ 6 x 6   +   x 2 é uma aproximação melhor do que s e n   x   ≈   x .

Vamos investigar o resultado acima comparando os gráficos de f   ( x )   =   s e n   x   -   x e g ( x )   =   s e n   x   -   6 x 6   +   x 2 .

Na figura abaixo, notamos que o gráfico de g ( x ) está próximo da linha y = 0 (eixo x). Assim, a partir do gráfico, podemos concluir que s e n   x   -   6 x 6   +   x 2 é uma aproximação melhor do que s e n   x -   x .

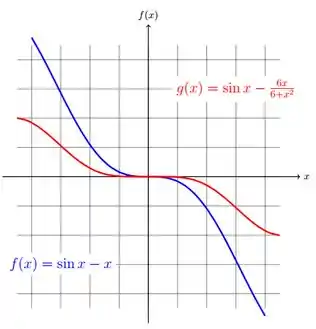
Para melhor compreensão traçando as três funções, temos:

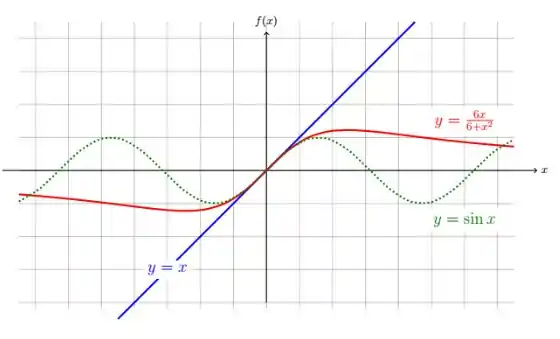
6 x 6   +   x 2 se assemelha mais à função s e n   x do que a função x .

Espero ter ajudado! Abraços e até a próxima!

Resposta

A função s e n   x   -   6 x 6   +   x 2 é uma aproximação melhor do que s e n   x -   x .

Exercícios de Livros Relacionados

O que é uma série de potências?
Nos Exercícios 1-36, (a) encontre o raio e o intervalo de convergência da série. Para quais valores de x a série converge (b) absolutamente? E (c) condicionalmente? ∑ n = 0 ∞ - 1 n 4 x + 1 n
O que é uma série de potências? Como você testa uma série de potências para convergência? Quais são os possíveis resultados?
Utilize uma representação em série de s e n3 x para encontrar valores de r e s para os quais. lim x → 0 ⁡ s e n3 x x 3 + r x 2 + s = 0