Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 40
Complete as identidades usando o método do triângulo (Figura )
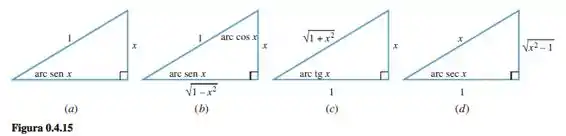
Passo 1
Fala povo, tudo ok? Olha só a questão já ajuda bastante a gente. Da figura que ela fala, temos:
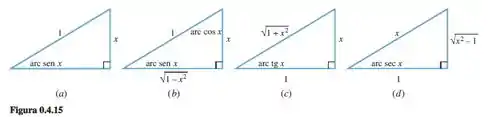
Note que dentro dela temos ângulos que já estão escritos em função dos lados! Portanto, pra resolvermos a questão, vai bastar olhar pro enunciado e escolher um triângulo que tenha esse ângulo escrito! Por exemplo, pra letra , temos:
E o triângulo da figura tem o arco “” escrito:
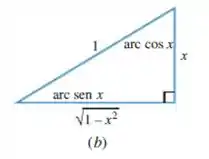
Pela figura, o seno desse ângulo vai ser o cateto oposto a ele (a base do triângulo) sobre a hipotenusa:
Pescou a ideia? Vamos fazer isso pras próximas letras então!
Passo 2
Letra b:
Olhando pra figura, podemos usar o mesmo triângulo do passo :
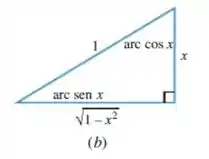
Pela figura, a tangente desse ângulo vai ser o cateto oposto a ele (a base do triângulo) sobre o cateto adjacente (a altura do triângulo):
Boaa! Próxima letra!
Passo 3
Letra e , respectivamente:
Agora a gente vai mudar o triângulo da figura pro triângulo , afinal ele é o único com “” escrito dentro. Dá uma olhada:
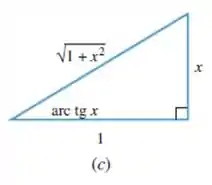
Como cossecante é o inverso de seno, vamos primeiro fazer o seno desse ângulo. O seno desse ângulo vai ser o cateto oposto a ele (a altura do triângulo) sobre a hipotenusa:
E logo, a cossecante será:
E nisso já respondemos as duas últimas letras visto que ambas usam o mesmo triângulo auxiliar!