O número de horas de claridade em um dado dia e em um dado ponto da superfície terrestre depende da latitude do ponto, do ângulo através do qual a Terra moveu-se em seu plano orbital durante o período de tempo a partir do equinócio de outono ( de março) e do ângulo de inclinação do eixo de rotação da Terra, medido a partir da eclíptica para o norte (). O número de horas de claridade pode ser aproximado pela fórmula
Em que:
E é medido em graus. Dado que Fairbanks, no Alaska, está localizado à latitude de e também que em de junho e em de dezembro, aproxime:
- O número máximo de horas de claridade em Fairbanks com uma casa decimal;
- O número mínimo de horas de claridade em Fairbanks com uma casa decimal;
Passo 1
Ô enunciado feio hahaha muita letra grega gente! Mas calma que vamos tirar de letra. A questão pede número máximo e mínimo de horas de claridade. Ou seja, o máximo e mínimo. Veja só galera, essa letrinha tem essa definição, dada pelo enunciado:
E a letra , tem essa:
Então deu pra ver que pra achar , precisamos primeiro achar . Vamos focar nisso!
Passo 2
Show, olha, a questão dá pra gente alguns outros dados:
- em de junho
- em de dezembro
Po galera, então dessas letras gregas, a única que varia é , sendo as outras constantes Como depende de , para:
Achamos então exatamente o valor máximo e mínimo que um seno pode obter! Sendo o resto da expressão de constante, máximo ou mínimo nos fornece valores de máximos ou mínimos também! Saca só, seja:
Substituindo as constantes e a variável, temos:
Podemos fazer isso com uma calculadora ou então usando uma ferramenta famosa de planilhas. Nela, montamos a fórmula de com cuidado, selecionando as células corretas e depois usamos a função “=ASEN()” pra calcular o arcoseno de . Os resultados são:
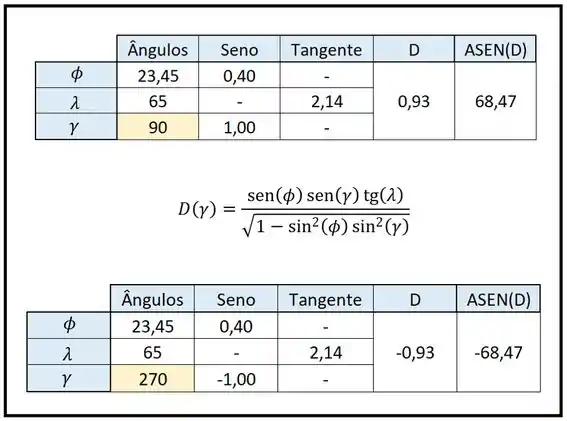
Passo 3
Agora pra fechar pessoal, vamos analisar esses valores de na fórmula do . Seja:
Para e usaremos a lei de formação do meio:
E de novo, podemos usar a ferramenta de planilhas pra achar esse resultado:
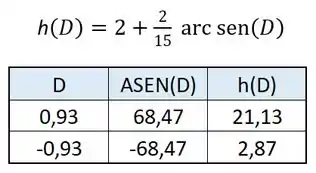
Ta na mão! Nossos máximos e mínimos serão, respectivamente, horas e horas!