a) Se deslocarmos uma curva para a esquerda, o que acontece com sua reflexão em torno da reta Em vista desse princípio geométrico encontre uma expressão para a inversa de , onde é uma função um a um.

b) Encontre uma expressão para a inversa de , onde .

Para entender o que vai acontecer com a nossareflexão em torno da reta , se deslocarmos uma curva para a esquerda, vamos supor uma função qualquer e desenhá-la junto da reta num eixo cartesiano.

Vamos escolher a função

Obs: poderia ser qualquer função, mas essa ficará de um lado só da reta e a gente vai poder ver com mais clareza. Ok?

Veja o gráfico dela:

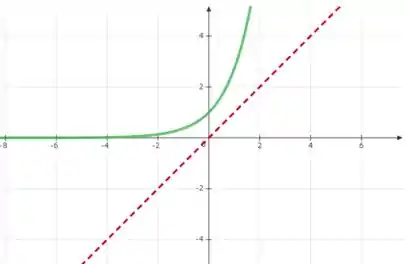
Agora vamos colocar também sua reflexão em torno da reta :

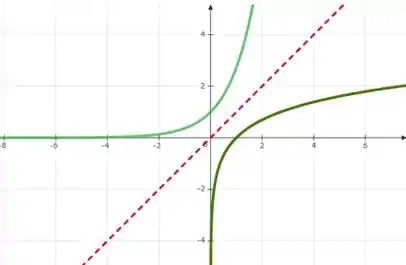
Agora vamos ver o que acontece se deslocarmos a curva para a esquerda. Vamos fazer isso em duas unidades.

Assim, nossa função será:

E veja nosso novo gráfico e sua nova reflexão em linha cheia abaixo:

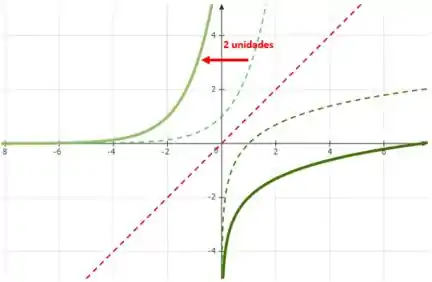
O que aconteceu com nosso reflexo é que ele também ficou deslocado, mas agora em 2 unidades para baixo. Veja:

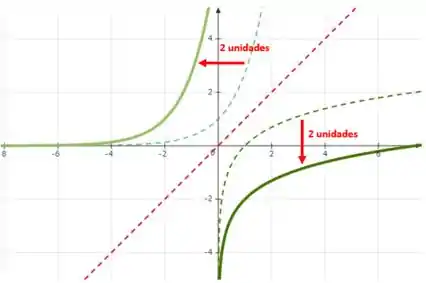
Assim, podemos concluir que:

Se deslocarmos uma curva para a esquerda, então, seu reflexo com relação a reta (função inversa) será deslocada a mesma quantidade de unidades para baixo. Assim, a expressão que o problema nos pede pode ser representada por:

Agora vamos ao item b)

temos que encontrar uma expressão para a inversa de , onde .

Perceba que quando multiplicamos a variável por um valor, causamos a compressão ou o alargamento da curva

Assim, se comprimirmos (ou esticarmos) uma curva de forma horizontal, o reflexo em relação a reta , ou seja, sua inversa será comprimida (ou esticado) de forma vertical por um mesmo fator. Então,

E prontinho, chegamos as nossas respostas.