Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 12
(i) Complete a tabela e dê um palpite sobre o limite indicado
(ii) Confirme suas conclusões sobre o limite desenhando o gráfico da função sobre um intervalo adequado
;
Passo 1
(i) Não tem mistério: aqui é só jogar os valores de da tabela na função e calcular . Agora, é claro que fazer isso na mão fica complicado. Sugiro que você use uma calculadora gráfica ou mesmo o Excel pra isso.
Jogando esses valores no Excel ou na calculadora, vamos ter então, respectivamente para :
Passo 2
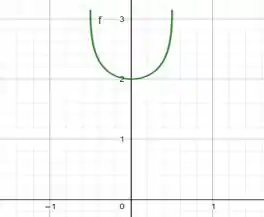(ii) Temos pra essa função o gráfico:
Precisamos agora confirmar o que vemos no gráfico calculando o limite. Nesse caso, podemos fazer isso facilmente pela regra de l’Hopital, que diz que o limite de uma função qeuivale ao limite da derivada dessa mesma função.
Mas, atenção: temos uma função quociente. Na regra de l’Hopital, nós derivamos o numerador e o denominador como funções diferentes, e não aplicamos a regra do quociente!
Vamos ter:
Podemos aplicar diretamente o valor de no lugar de e calcular o limite. Teremos:
Quando olhamos no gráfico, confirmamos que, de fato, quando nos aproximamos de , a função tende a 2!
Resposta
Ei, a resposta está no passo a passo :)