Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.2 - Ex. 81a

Componha uma série infinita de termos diferentes de zero cuja soma seja:

a. 1

Passo 1

Olá galerinha, vem fazer esse exercício comigo! Primeiramente iremos relembrar que para uma dada série ∑ n = 1 ∞ a n = a 1 + a 2 + a 3 + ⋯ , denote por s n sua n -ésima soma parcial:

s n = ∑ i = 1 ∞ a i = a 1 + a 2 + ⋯ + a n

A série ∑ n = 1 ∞ 1 n ( n + 1 )   é   um série convergente com a seguinte soma parcial:

s n = ∑ i = 1 n 1 i ( i + 1 ) = 1 1 ∙ 2 + 1 2 ∙ 3 + 1 3 ∙ 4 + ⋯ + 1 n n + 1

Podemos simplificar essa expressão se usarmos a decomposição em frações parciais:

1 i ( i + 1 ) = 1 i - 1 i + 1

Sendo assim:

s n = ∑ i = 1 n 1 i ( i + 1 ) = ∑ i = 1 n 1 i - 1 i + 1

= 1 - 1 n + 1

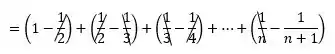
Então temos o seguinte:

lim n → ∞ ⁡ s n = lim n → ∞ ⁡ 1 - 1 n + 1 = 1 - 0 = 1

Portanto:

∑ n = 1 ∞ 1 n ( n + 1 ) = 1

Então essa é uma série infinita cuja soma é 1.

Resposta

∑ n = 1 ∞ 1 n ( n + 1 ) .

Exercícios de Livros Relacionados

Calcule a soma indicada, usando os Teoremas 5.4.2 até 5.4.7 ∑ i = 1 n ( 10 i + 1 - 10 i )
Ache a soma dadasum_(i = 1)^7 (i + 1)^2
Calcule a soma indicada, usando os Teoremas 5.4.2 até 5.4.7 ∑ i = 1 20 3 i ( i 2 + 2 )
Suponha que sum_(k = 1)^(20) a_k = 0 e sum_(k = 1)^(10) b_k = 7 . Determine o valor de sum_(k = 1)^(20) 3 a_k
Suponha que sum_(k = 1)^(10) a_k = - 2 e sum_(k = 1)^(10) b_k = 25 . Determine o valor de sum_(k = 1)^(10) (a_k + b_k - 1)