Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 30

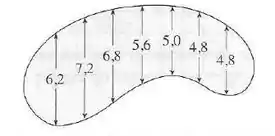
Os comprimentos (em metros) de uma piscina com o formato de um rim são medidos a intervalos de 2 metros, como indicado na figura. Use a Regra de Simpson para estimar a área da piscina.

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente estimar a área dessa piscina em formato de rim, sabendo que os vários comprimentos que tem ali dentro são medidos em intervalos de 2   m cada um.

Observe que temos 7 medições a cada 2   metros, então, começando em 0 e temos um comprimento de 16   m . Chamando esse comprimento de x , sua variação será Δ x = 2 e o nosso intervalo pode ser escrito na forma:

0 ≤ x ≤ 16

Agora, como ele quer que usemos a Regra de Simpson para estimar essa área, vamos precisar da fórmula:

S n = f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + ∙ ∙ ∙ + 2 f x n - 2 + 4 f x n - 1 + f x n ∆ x 3

Onde f ( x n ) serão as nossa medições no intervalo considerado. Então, basta substituir os valores na fórmula e calcular.

Vamos lá!

Passo 2

Partindo de zero até 16 , indo de dois a dois, vamos ter as medições:

f 0 = 0

f 2 = 6,2

f 4 = 7,2

f 6 = 6,8

f 8 = 5,6

f 10 = 5,0

f 12 = 4,8

f 14 = 4,8

f 16 = 0

Além disso, Δ x = 2 . Então, substituindo tudo na fórmula, teremos:

S 8 = ∆ x 3 f 0 + 4 f 2 + 2 f 4 + 4 f 6 + 2 f 8 + 4 f 10 + 2 f 12 + 4 f 14 + f 16

S 8 = 2 3 0 + 4 ∙ 6,2 + 2 ∙ 7,2 + 4 ∙ 6,8 + 2 ∙ 5,6 + 4 ∙ 5,0 + 2 ∙ 4,8 + 4 ∙ 4,8 + 0

Resolvento isso, temos:

S 8 ≈ 84

Portanto, a nossa área é aproximadamente 84   m 2 .

Valeu, galera! Até a próxima! 😉

Resposta

A = 84   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tronco de 10m de comprimento é cortado a intervalos de 1m e as suas áreas de secção transversal A (a uma distância x da extremidade do tronco) estão listadas na tabela. Use a Regra do Ponto Médio c
Há um fluxo de água para dentro e para fora de um tanque de armazenamento. A seguir, temos um gráfico que mostra a taxa de troca r t do volume de água no tanque, em litros por dia. Se a quantidade de
A velocidade de um carro foi lida de seu velocímetro em intervalos de 10 segundos e registrada na tabela. Use a Regra do Ponto Médio para estimar a distância percorrida pelo carro.
Suponha que um vulcão esteja em erupção e que as leituras da taxa r t com que materiais sólidos são lançados na atmosfera sejam as dadas na tabela. O tempo t é medido em segundos e a unidade para r t
Expresse o limite como uma integral definida. lim n → ∞ ⁡ ∑ i = 1 n i 4 n 5 [Sugestão: Considere f x = x 4 .]