Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 9
Encontre os valores máximo e mínimo absolutos de nos intervalos fechados dados e indique onde ocorrem esses valores
9.
Passo 1
Os pontos críticos são calculados primeiramente fazendo a derivada e achando quando que ela é igual a zero, então derivando , pela regra da cadeia, temos:
E quando
Temos que é um ponto crítico
Passo 2
Agora falta descobrir se é um ponto de máximo ou mínimo. Para isso vamos fazer o teste da primeira derivada, vamos pegar um ponto a esquerda de 4 e um a direita de 4
e
Entao, nesse caso a derivada antes é positiva e depois também, então o ponto não é um ponto crítico, não sendo nem um “topo da colina” nem um “buraco”, nesse caso. Outra maneira de analisar o tipo de ponto crítico é fazendo o teste da segunda derivada, se então o ponto é máximo, se então o ponto é mínimo, se é inconclusivo
Passo 3
Vamos fazer o teste da segunda derviada para descobrir o que é esse ponto.
Então não podemos concluir se é um ponto de máximo e mínimo por esse método, analisando o gráfico temos uma função do 3º grau, que seu gráfico é esse aqui:
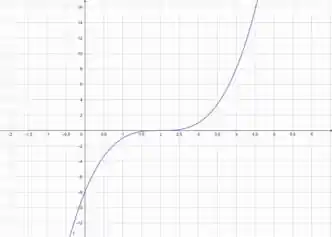
Conseguimos ver que o ponto não é um ponto de máximo nem mínimo, e que a função está sempre crescendo, então, no intervalo de , o ponto máximo é em e o mínimo em .
Resposta
Ei, a resposta está no passo a passo :)