Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 54b
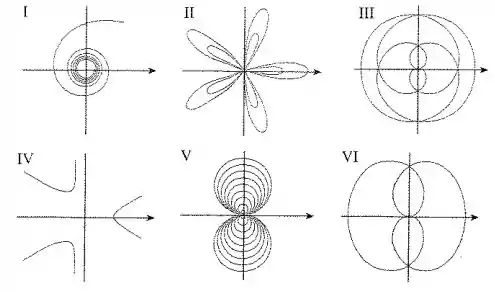
Conecte as curvas polares com seus respectivos gráficos I-VI.
Passo 1
A questão pede para ligarmos a curva dada em coordenadas polares a um dos gráficos disponíveis.
Neste caso, temos
A gente precisa analisar alguns pontos e comportamentos na função e no gráfico para encontrarmos quem é quem. Precisamos olhar para raízes, pontos de periodicidade, etc.
Note que vai completar um ciclo completo quando rodar de a :
Portanto, devemos ter uma curva que executa voltas completas!
Passo 2
A única curva que executa quatro voltas é a curva . Só pode ser ela!
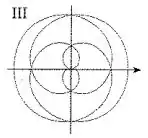
Resposta
III
Exercícios de Livros Relacionados
Investigue a família de curvas definidas pelas equações paramétricas x = s e ntc - s e nt y = cos t( c - s e nt )
Encontre três conjuntos diferentes de equações paramétricas para representar a curva y = x 3 , x ∈ R .
a) Elimine o parâmetro para encontrar uma equação cartesiana da curva.b) Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = 1 + cos θ , y = 2 c
a) Elimine o parâmetro para encontrar uma equação cartesiana da curva.b) Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = s e n 2 θ , y = cos 2
Descreve o movimento de uma partícula com posição ( x ,y ) quando t varia no intervalo dado. x = 2s e nt , y = 3 cos t ,0 ≤ t ≤ 2 π