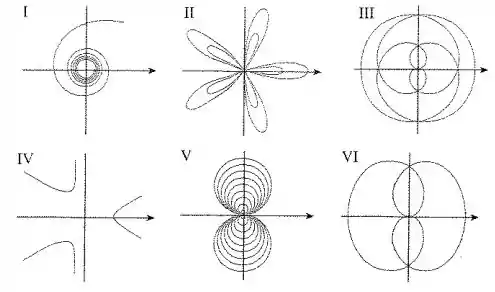
Conecte as curvas polares com seus respectivos gráficos I-VI.
Passo 1
A questão pede para ligarmos a curva dada em coordenadas polares a um dos gráficos disponíveis.
Neste caso, temos
Note que vai completar um ciclo completo quando rodar de a :
O que iremos fazer para conseguirmos encontrar qual o gráfico dessa função é analisarmos os pontos importantes, como raízes, ponto de interseção aos eixos, periodicidade, são esses pontos que nos ajudam a encontrarmos os gráficos.
Passo 2
Para
Temos
de modo que a curva começa na origem.
Daí, conforme vai de até , vai de até 1, sempre crescendo!
Em seguida, quando vai de até , continua positivo, porém vai diminuindo de até chegar em quando : a curva volta para a origem!
Passo 3
Agora vamos para a segunda volta:
nela,
de modo que .
Desta forma, sempre temos que rebater a curva para o quadrante oposto!
Para
começa no e acaba no , de modo que a curva parte no terceiro quadrante e depois passa pelo quarto terminando no ponto (coordenadas cartesianas).
Por fim, entre e , vai de até , executando uma trajetória simétrica acima do eixo .
O gráfico que melhor descreve toda essa bagunça é o VI.
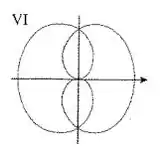
Resposta
VI