Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 30

Esboce a área da região que está dentro de ambas as curvas.

r = s e n   2 θ ,               r = s e n   θ

Passo 1

O problema pede para acharmos a área da região dentro das curvas r = s e n   2 θ e r = s e n   θ .

Um esboço das duas curvas é dado a seguir:

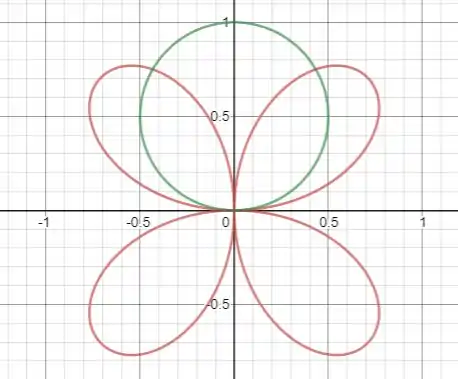
Note que a região pedida é dividida em duas partes idêntica: uma à direita do eixo y e outra à esquerda!

Assim, vamos focar na região do primeiro quadrante e depois multiplicar sua área por 2 .

A área abaixo do gráfico é uma integral, é dada por:

A = 1 2 ∫ b a r 2 d θ

Em que a ,   b é o intervalo de integração.

Passo 2

Vamos procurar o ponto de encontro entre as curvas no primeiro quadrante:

r = s e n   2 θ r = s e n   θ

Assim,

s e n   2 θ = s e n   θ

2   s e n   θ cos ⁡ θ = s e n   θ

s e n   θ = 0   ; cos ⁡ θ = 1 2

Portanto, o ponto de encontro das curvas que vai servir de fronteira para as integrais é

θ = π 3

A área da região no primeiro quadrante é o somatório das áreas na região:

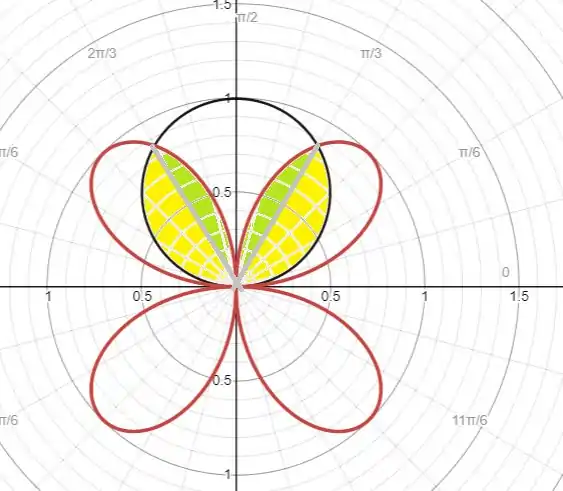
Observe a parte amarela sombreada. É delimitada pela curva do círculo de  0  Para π 3 . Agora, observe a parte verde sombreada. É delimitada pela curva da rosa de  π 3 ​ para  π 2 .

A p r i m .   q u a . = ∫ 0 π / 3 1 2 r v e r d e 2 d θ + ∫ π / 3 π / 2 1 2 r v e r m e l h o 2   d θ

Assim,

A p r i m .   q u a . = ∫ 0 π / 3 1 2 s e n 2 θ   d θ + ∫ π / 3 π / 2 1 2 s e n 2 2 θ   d θ

Como a área que queremos é o dobro dessa:

A = ∫ 0 π / 3 s e n 2 θ   d θ + ∫ π / 3 π / 2 s e n 2 2 θ   d θ = I 1 + I 2

Vamos calcular I 1 primeiro:

Vamos utilizar a identidade:

sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2

Substituindo na integral:

I 1 = 1 2 ∫ 0 π 3 1 - cos ⁡ 2 θ   d θ

I 1 = 1 2 ∫ 0 π 3 1 d θ - ∫ 0 π 3 cos ⁡ 2 θ d θ

Integrando, temos:

I 1 = 1 2 θ - 1 2 s e n   2 θ 0 π / 3

Logo,

I 1 = 1 2 π 3 - 1 2 s e n 2 π 3

I 1 = π 6 - 3 8

Passo 3

Para I 2 , fazemos a mudança de variável:

x = 2 θ

d θ = d x 2

Precisamos mudar também os limites de integração:

x = 2 π 3

x = π

Assim,

I 2 = 1 2 ∫ 2 π 3 π s e n 2 x   d x

Vamos utilizar a identidade:

sin 2 ⁡ x = 1 - cos ⁡ 2 x 2

I 2 = 1 4 ∫ 2 π 3 π 1 - cos ⁡ 2 x d x

I 2 = 1 4 ∫ 2 π 3 π 1 - cos ⁡ 2 x d x

Resolvendo nossa integral:

I 2 = 1 4 x - 1 2 s e n   2 x 2 π 3 π

Logo,

I 2 = 1 4 π 3 + 1 2 s e n 4 π 3

I 2 = π 12 - 3 16

Assim,

A = I 1 + I 2

A = π 6 - 3 8 + π 12 - 3 16

Portanto,

A = π 4 - 3 3 16

Resposta

A = π 4 - 3 3 16

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da região sombreada na figura a seguir.Parece que, se o gráfico de r = t gθ ,- π 2θπ 2 , poderia ser assintótico às retas x = 1 e x = - 1 . Sim ou não? Justifique sua resposta.
Circunferências dos círculosComo é usual diante de uma nova fórmula, é uma boa ideia testá-la em objetos familiares para ter a certeza de que ela fornece resultados consistentes com a experiência pass
r = f θ contra r = 2 f ( θ ) Alguma coisa pode ser dita sobre os comprimentos relativos das curvas r = f θ ,α ≤ θ ≤ β , e r = 2 f θ ,α ≤ θ ≤ β ? Justifique sua resposta.
Valor médioSe f é continua, o valor médio da coordenada polar r sobre a curva r = f θ ,α ≤ θ ≤ β , com relação a θ é dado pela formula: r m = 1 β - α ∫ α β f θ d θ Utilize essa formula para encontrar
Comprimento da curva r = f θ ,α ≤ θ ≤ β Assumindo que as derivadas necessárias são continuas, mostre como as substituições x = f θ cos ⁡ θ ,y = f θ s e nθ (equações 2 no texto) transformam L = ∫ α β d