Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.10 - Ex. 12
Seja para
- Determinar
- Qual o domínio da função
- Determinar e indicar o domínio.
- Determinar
- Traçar o gráfico de
Passo 1
- Vamos lá, aqui é só substituir os valores e calcular...
- Bom, o domínio são os valores que podem assumir, nesse caso é:
- Vamos substituir aqui:
- Aqui a gente faz primeiro e depois aplica na função de novo:
- Agora só falta o gráfico:
não existe né, porque o
E também não existe pelo mesmo motivo😊
Passo 2
Passo 3
Pra ver o domínio, a gente faz:
Ou seja, o domínio é: .
Passo 4
não tem, porque o domínio só vai até .
Passo 5
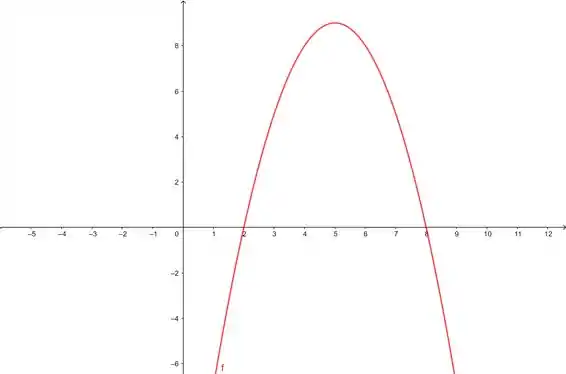
Prontinho😊
Resposta
Exercícios de Livros Relacionados
22.Sendo f ( x ) = a x + b , para os quais valores de a e b tem-se ( f o f ) ( x ) = 4 x - 9 .
26.A função g é definida por g ( x ) = x 2 . Defina uma função f tal que ( f o g ) ( x ) = x , para x ≥ 0 e uma função h , talque ( h o g ) ( x ) = x , para x ≤ 0 .
24.Sejam f ( x ) = 5 x,x ≤ 0 - x ,0x ≤ 8 x ,x8 e g ( x ) = x 3 . Calcular f o g .
28.Se f ( x ) = x 2 - 2 x + 1 , encontre uma função g ( x ) para os quais ( f / g ) ( x ) = x - 1 .
29.Ddas as funções f ( x ) = x 2 - 1 e g ( x ) = 2 x - 1 : ( a ) Determine o domínio e conjunto imagem de f ( x )