Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.4 - Ex. 2a
Considerando que a superfície é obtida girando a curva , , em torno do eixo , pede-se
- Uma parametrização para
Passo 1
Veja a figura abaixo:
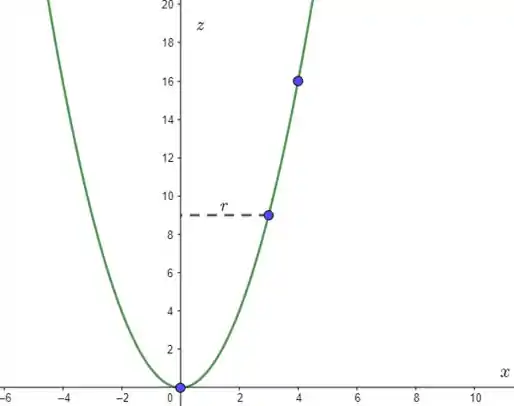
Note que estamos no plano !! Como girarmos a curva ao redor do eixo , então formaremos vários círculos paralelos ao plano de raio , com .
Passo 2
Portanto, uma boa parametrização é:
Note que o intervalo garante que percorremos cada circulo inteiramente.
Resposta
Uma parametrização é .
Exercícios de Livros Relacionados
Calcular a área da parte do cone z 2 = x 2 + y 2 que está no interior do paraboloide z = 2 x 2 + 2 y 2 .
Calcular a área da parte da esfera x 2 + y 2 + z 2 = 16 interior ao cilindro y 2 + z 2 = 4 z .
Encontrar a área da superfície do cilindro x 2 + z 2 = 25 limitada pelos planos x = 0 , x = 2 , y = 0 , y = 3 .
Determinar a área da superfície plana x + y + z = 8 delimitada pelo cilindro x 2 + y 2 = 4
Calcular a área da parte da esfera x 2 + y 2 + z 2 = 9 que está no interior do cilindro x 2 + y 2= 4