Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.6 - Ex. 2b
Considere a aplicação definida pelas equações
e
Descreva e esboce a região .
Passo 1
Bom galera, a gente precisa transformar a região do plano em uma região do plano . Onde temos que:
E a região é:
Passo 2
Belezinha, vamos mexer um pouquinho nas nossas equações para deixar uma apenas em função de e outra apenas em função de :
Agora delimitamos a nossa região :
Passo 3
Show de bolinhas, agora com o que a gente encontrou a gente pode delimitar a região gráficamente:
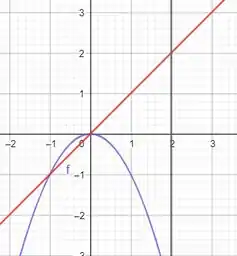
E prontinho. 😊
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejam σ : Ω ⊂ R 2 → R 3 e φ : Ω 1 ⊂ R 2 → R 3 duas superfícies regulares, sendo φ obtida de σ pela mudança de parâmentros u , v = H s , t = u s , t , v s , t (veja exercício anterior). Sejam K ⊂ Ω e K
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .
Considere a aplicação definida por x = u v e y = v - u Calcule a a área de D .