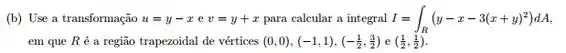Exercícios de Mudança Qualquer de Variáveis - Lista de Exercícios Resolvida

Seja . Calcular o valor da integral

Considere a aplicação definida por:

Utilizando , calcule , onde é a imagem no plano da região no plano limitada pelas retas , e .

Calcule onde é a região do primeiro quadrante do plano , limitada pelas curvas , , e .

Calcule onde é a região do plano limitada pelas retas , , e .

Calcule

Onde é o paralelogramo de vértices , , e .

Sugestão: faça uma mudança de variáveis conveniente.

Calcule a integral dupla , onde é a região delimitada pelas curvas dadas pelas equações , , e .

Calcule

Onde

Sugestão: considere a mudança de variáveis satisfazendo e .

Calcule

Onde é a região limitada pelas retas , , e .

Calcule , onde é limitado por , , , .

Obs: o enunciado dessa questão foi alterado, com relação ao original disponibilizado pelo Instituto de Matemática e Estatística da Universidade.

Calcule , sendo a região do plano limitada por:

Calcule

Em que é a região trapezoidal com vértices , , , .

Seja . Calcule

1. Calcule as seguintes integrais:

é a região triangular de vértices .

Considere a integral

onde é a região limitada pelas , , e .

Desenhe a região de integração. Justifique...

Calcule a integral . Justifique...

Utiliza a transformação dada para calcular a integral

b) , onde é a região no primeiro quadrante limitada pelas retas e e as hipérboles , ; , .

Calcule a integral, efetuando a mudança de variáveis apropriada

a) , onde é a região do primeiro quadrante limitada pela elipse .

Calcule

Sendo a região do plano limitada por , , , .

Questão 1. Calcule a integral dupla

onde

Seja a região delimitada pelo quadrilátero com vértices , , e .

a) Esboce a região no plano .

b) Considere a transfomação e . Esboce a imagem da região através da tranformação no plano .

c) Calcule

Calcule , onde

(Sugestão: Faça e )

. Seja o paralelogramo com vértices , , e . Usando a mudança de variável e , calcule a integral.

Utiliza a transformação dada para calcular a integral

a) , onde é a região triangular com vértices , e ; , .

Calcule a integral, efetuando a mudança de variáveis apropriada

a) , onde é o paralelogramo limitado pelas curvas , , e .

Calcule, efetuando uma mudança de variáveis conveniente, a integral

Onde é a região trapezoidal com vértices , , e .

Use a mudança de coordenadas

para calcular a integral

Onde é o polígono de vértices e .

Calcule

Onde é a região trapezoidal com vértices , , e .

Calcule as seguintes integrais

é o quadrado

Considere a integral

Onde é a região do primeiro quadrante limitada pelas retas , , e .

Usando a mudança de variáveis com e , calcule .

Calcule onde é a região no primeiro quadrante do plano limitada pelas curvas , , e

Considere a região limitada pela curva e pelos eixos coordenados. Determine

Dica: utilize a transformação de coordenadas , .

1) A mudança de variáveis que tem como Jacobiano

É:

Calcule a integral dupla

Onde é o trapezoide com vértices , , , .

Dica: Faça uma mudança de variáveis para simplificar o integrando.

3 – Calcular:

Em que é a região delimitada por .

1) A integral de na região definida por e é igual a

Questão 2: Calcule a integral

Onde é a região no primeiro quadrante limitada pelas hipérboles , e pelas curvas , .

Sugestão: use coordenadas adequadas.

Questão 3: Seja a região e considere uma mudança de variáveis de em que satisfaça às equações

Seja a região do plano com coordenadas , tal que .

1. Esboce as regiões e . Assinalem em seus esboços da região pontos , , e na fronteira das curvas que limitam a região e, no esboço da região , assinale suas imagens correspondentes , , e . Não é necessário calcular explicitamente as coordenadas dos pontos, embora possa ser desejável para verificar as contas.
2. Escreva uma fórmula para , calcule a matriz Jacobiana e seu determinante.
3. Use a mudança de variáveis para calcular

Sejam o paralelogramo de vértices e funções contínuas em . É corrento concluir que

no caso em que

Considere a região do plano

1. Desenhe R hachurado. Desenhe ao lado a fronteira de R, denotada por Fr(R).
2. Considere a integral dupla(i) Escreva usando obrigatoriamente uma integral iterada, integrando primeiro com respeiro a y e em seguida com a respeito a x.Obs: Neste item não é para calcular o valor numérico de , apenas escrever a forma pedida.

(ii) Escreva usando obrigatoriamente uma integral iterada, integrando primeiro com respeito a x e em seguida em respeito a y.

Obs: Neste item não é para calcular o valor numérico de , apenas escrever a forma pedida.

3. Calcule
4. Considere

Calcule o volume de .

Calcule a integral dupla

Onde é o paralelogramo de vértices , , e . Considere a mudança de variáveis e .

Considere a integral

Onde .

1. Usando a mudança de variáveis , esboce cuidadosamente a região tal que , justificando.
2. Calcule a derivada .
3. Calcule a integral dada usando a fórmula de mudança de variáveis.
4. Cheque o resultado do item (c) calculando a integral nas variáveis .

Considere e a integral dada por

1. Usando mudança de variáveis , encontre a região tal que e esboce e
2. Determine a matriz jacobiana
3. Calcule a integral dada usando a fórmula de mudança de variáveis para . Justifique.

Considere a integral

Onde é o triangulo de vértices nos pontos , e

1. Usando a mudança de variáveis com e , encontre a região tal que e esboce e
2. Determine a matriz jacobiana .
3. Mostre que é injetora
4. Calcule a integral dada usando a fórmula de mudança de variáveis

Seja a região plana no primeiro quadrante compreendida pelo gráfico das funções , , e .

1. Usando a mudança de variáveis e , determine a transformação e calcule a matriz jacobiana de .
2. Determine a região do plano cuja imagem pela transformação é .
3. Use a fórmula de mudança de variávies para provar que

Onde é uma função tal que

Seja uma função contúnua. Utilizando uma mudança de variáveis apropriada, mostre que

Onde é a região do primeiro quadrante limitada pelas linhas de equação , , e .

Calcule a seguinte integral

é a região do primeiro quadrante, limitada pelas parábolas , , e

Calcule a integral

onde é a região limitada pelas hipérboles no semiplano direito.

Sugerão: Use a transformação e calcule o Jacobiano usando o fato de que , onde . E mostre que

Calcule a integral dupla

Onde . Sugestão: use mudança de variáveis.

a) Esboce a região

b) Efetuando uma mudança de variáveis apropriada, calcular a integral

Dica: considerar e determinar tal que a mudança de variáveis simplifique o domínio de integração.

Calcule a integral dupla

Onde é a região, no primeiro quadrante, limitada pelas curvas , , , e .

Seja a região do primeiro quadrante limitada por , , e e seja a mudança de variáveis onde

a) Esboce a região e a região tal que .

b) Usando a mudança de variáveis calcular a integral

. Seja o paralelogramo com vértices , , e . Usando a mudança de variável e , calcule a integral.

A integral iterada vale

a)

b)

c)

d)

e)

Considere a integral

Onde é o paralelogramo delimitado pelas retas , , e .

1. Escolha uma mudança de variáveis apropriada (note que . Calcule a derivada .
2. Esboce cuidadosamente as regiões de integração , onde .
3. Calcule a integral usando a fórmula de mudança de variáveis.

Seja a região triangular do plano com vértices nos pontos e .

1. Considere a mudança de variáveis e esboce a região do plano tal que
2. Calcule o Jacobiano da mudança de variáveis
3. Seja a função

Calcule a integral .

Calcule a integral, efetuando uma mudança de variáveis apropriada.

Onde é a região trapezoidal com vértices: