Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.6 - Ex. 9
Considere uma barra de alumínio, com 20 cm de comprimento, inicialmente a uma temperatura uniforme de 25°C. Suponha que, no instante t = 0, a extremidade x = 0 é esfriada a 0°C, enquanto a extremidade x = 20 é aquecida a 60°C, e ambas são mantidas, daí para frente, a essas temperaturas.
- Encontre a distribuição de temperatura na barra em qualquer instante t.
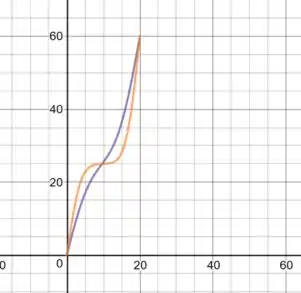
- Faça os gráficos da distribuição inicial de temperatura, da distribuição final (estado estacionário) e de duas distribuições em dois instantes representativos intermediários no mesmo conjunto de eixos.
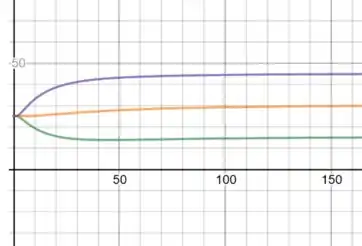
- Faça o gráfico de u em função de t para x = 5, 10 e 15.
- Determine o intervalo de tempo necessário para que a temperatura em x = 5 cm alcance um intervalo de 1% (e permaneça nesse intervalo) em torno de seu valor no estado estacionário.
Passo 1
Letra a:
Temos as seguintes condições:
Para , a partir da tabela 10.5.1 na página 624, temos que
A solução para esse problema é dada pelas fórmulas 16 e 17 na página 634:
Para encontrar :
Então:
Passo 2
Letra b:
Início:
Final:
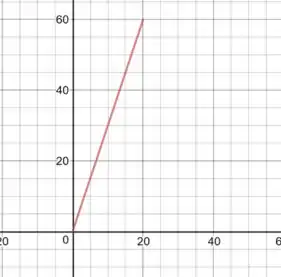
Dois tempos intermediários:
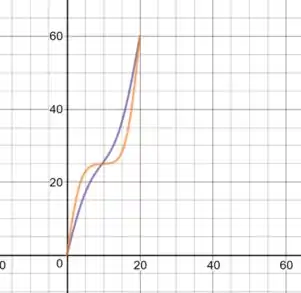
Passo 3
Na letra c:
u versus t, para x=5, x=10, x=15
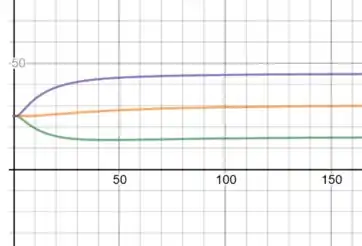
Passo 4
Na letra d:
Como concluímos que o estado estacionário da solução é 3x, ou x=5,15
Podemos observar o gráfico de u versus t da solução para x = 5 e procurar o tempo t de modo que a solução esteja dentro de 1% de 15. Podemos mover o ponto no gráfico para ver que na primeira vez a solução está dentro é .
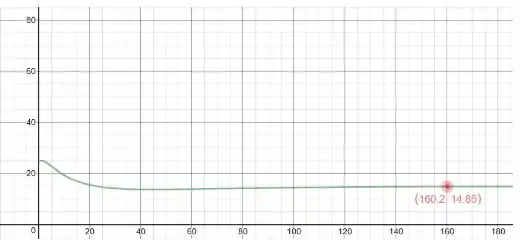
Resposta
