Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.2 - Ex. 17

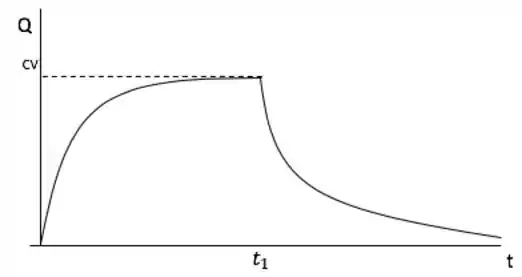
Considere um circuito elétrico contendo um capacitor, um resistor e uma bateria; veja figura 1.2.3. A carag Q(t) no capacitor satisfaz a equação

R d Q d t + Q C = V

Em que R é a resistência, C a capacitância e V é a voltagem constante forneceida pela bateria.

a) Se Q(0)=0, encontre Q(t) em qualquer instante t e esboce o gráfico de Q em função de t.

b) Encontre o valor limite Q L   para onde Q(t) tende após um longo período de tempo.

c) Suponha que   Q t 1 = Q L e que, no instante t   = t 1 , a bateria é removida e o circuito fechado novamente. Encontre Q(t) para t > t 1 e esboce seu gráfico

Passo 1

a) como nos foi dada a edo que representa o processo, vamos trabalhar em cima dela.

R d Q d t + Q C = V

Vamos resolver pelo método do fator integrante

Multiplicamos por μ t ambos os lados da equação e ficamos com:

μ t   d Q d t + μ t   Q R C = μ t V R

De modo que

d μ t d t = μ t R C

Portanto,

d μ t μ t = d t R C = d ln ⁡ μ t   ⟹ ln ⁡ μ t   = t R C     ⟹ μ t = e t / R C  

Substituindo na nossa edo, segue que

d e t R C × Q d t =   e t / R C   × V R   ⟹   e t R C × Q =   V R ∫ e t R C d t    

⟹ Q t = V R R C × e t R C + C 1 e t R C = C V + C 1 e t R C

Usando o nosso valor inicial , chegamos que C 1 = - C V

Portanto

Q t = C V 1 - e - t R C

b) Quando   t   →   ∞   ⟹ Q t = C V = Q L

Passo 2

c) A todo instante podemos dizer que

- R d Q d t   = Q C

ln ⁡ Q t C V = - t - t 1 R C

Q t = C V e - t - t 1 R C    

Resposta

Q t = C V 1 - e - t R C

Q t = C V = Q L

Q t = C V e - t - t 1 R C    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-4, mostre que cada função y = f ( x ) é uma solução da equação diferencial que a acompanha.4. y = 1 1 + x 4 ∫ 1 x 1 + t 4 d t ,y ' + 2 x 3 1 + x 4 y = 1
Nos Exercícios 1-4, mostre que cada função y = f ( x ) é uma solução da equação diferencial que a acompanha.1. 2 y ' + 3 y = e - x b) y = e - x + e - 3 2 x
Nos Exercícios 1-4, mostre que cada função y = f ( x ) é uma solução da equação diferencial que a acompanha.2. y ' = y ² ²b) y = - 1 x + 3
Nos Exercícios 1-4, mostre que cada função y = f ( x ) é uma solução da equação diferencial que a acompanha.1. 2 y ' + 3 y = e - x a) y = e - x
Nos Exercícios 1-4, mostre que cada função y = f ( x ) é uma solução da equação diferencial que a acompanha.3. y = 1 x ∫ 1 x e t t d t ,x 2 y ' + x y = e x