Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.5 - Ex. 11
Considere a condução de calor em uma barra com 40 cm de comprimento cujas extremidades são
mantidas à temperatura 0°C para todo . Em cada um dos problemas de 9 a 12, encontre uma
expressão para a temperatura u(x, t) quando a distribuição de temperatura inicial na barra for igual à função dada. Suponha que .
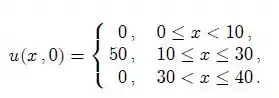
Passo 1
A solução geral desse problema é:
Então, precisamos achar os coeficientes que são os coeficientes senoidais de Fourier de Então:
Portanto, a solução do problema é (basta substituir o ):
Resposta
Exercícios de Livros Relacionados
Considere uma barra metálica com 20 cm de comprimento, aquecida a uma temperatura uniforme de 100°C. Suponha que, em t = 0, as extremidades da barra estão mergulhadas em um banho gelado a 0°C e depois
Considere novamente a barra do Problema 9. Para t = 5 e x = 20, determine quantos termos são necessários para encontrar a solução correta até três casas decimais. Um modo razoável de fazer isso é enco
Siga as instruções no Problema 14 para a barra no Problema 11.
Para a barra no Problema 19: Faça o gráfico de u em função de x para t = 5, 10, 20, 40, 100 e 200. Coloque todos os gráficos no mesmo conjunto de eixos, obtendo, assim, uma visão de como a distribuiçã