Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.5 - Ex. 16
Siga as instruções no Problema 14 para a barra no Problema 11.
Passo 1
A solução do problema é:
Na letra a, para t=5,10,20,40,100,200:
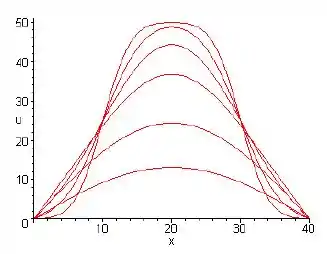
Passo 2
Na letra b:
Para x=5,10,15,20:
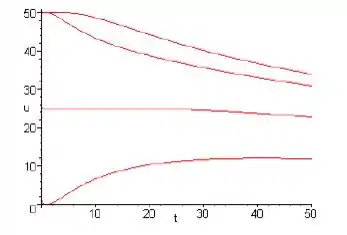
Passo 3
Na letra c:
A superfície de :
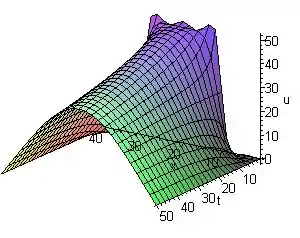
Passo 4
Na letra d:
para
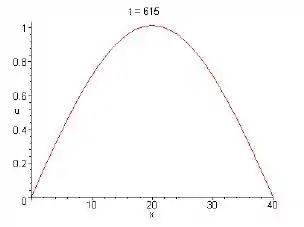
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere a condução de calor em uma barra com 40 cm de comprimento cujas extremidades são mantidas à temperatura 0°C para todo t0. Encontre uma expressão para a temperatura u(x, t) quando a distribui
Encontre a solução do problema de condução de calor 100 u x x = u t ,0x1 ,t0 ; u ( 0 , t ) = 0 ,u ( 1 , t ) = 0 ,t0 ; u ( x , 0 ) = s e n 2 π x - s e n 5 π x ,0 ≤ x ≤ 1
Considere a condução de calor em uma barra com 40 cm de comprimento cujas extremidades sãomantidas à temperatura 0°C para todo t0 . Em cada um dos problemas de 9 a 12, encontre umaexpressão para a tem
Encontre a solução do problema de condução de calor u x x = 4 u t ,0x2 ,t0 ; u ( 0 , t ) = 0 ,u ( 2 , t ) = 0 ,t0 ; u ( x , 0 ) = 2 s i n ( π x 2 ) - s i n π x + 4 s i n 2 π x ,0 ≤ x ≤
A equação do calor em duas dimensões espaciais é: α 2 ( u x x + u y y ) = u t Supondo que u ( x , y , t ) = X ( x ) Y ( y ) T ( t ) , encontre as equações diferenciais ordinárias satisfeitas por X ( x