Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.4 - Ex. 15
Considere a curva
- Esboce a parte da curva entre
- Explique por que a Fórmula (4) não pode ser usada para encontrar o comprimento da curva esboçada em (a).
- Encontre o comprimento de arco da curva esboçada em (a).
Passo 1
E aí, tudo joia?
- Vamos começar esboçando a curva:
- A fórmula 4, que é:
- Pra calcular então, a gente vai ter dividir em duas partes e colocar essa função sendo uma função de
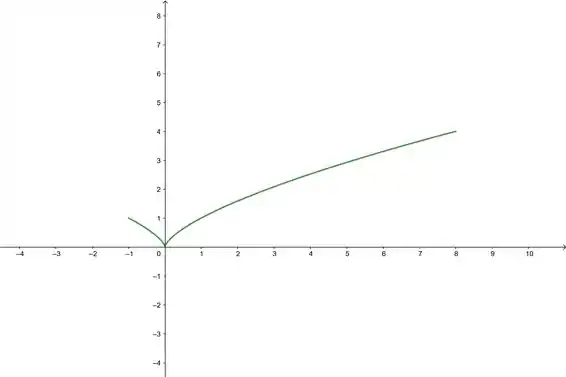
Tá aí! esse é o esboço da curva no intervalo pedido😊
Passo 2
Não pode ser aplicada, por que a derivada não existe no ponto , então ela não é contínua.
Passo 3
E aí usamos o intervalo de e de em , como vemos no gráfico.
Derivando a função, temos:
Aí as integrais ficam:
Passo 2
Resolvendo as integrais agora:
Fazemos uma substituição:
Agora voltamos para a variável :
E pronto! Calculamos o comprimento da curva😉
Resposta
Exercícios de Livros Relacionados
Determine os comprimentos das curvas nos Exercícios 17-20.20. x = ( y 3 / 12) + ( 1 / y ) , 1 ≤ y ≤ 2
Determine os comprimentos das curvas nos Exercícios 17-20.18. x = y 2 / 3 , 1 ≤ y ≤ 8
Determine o comprimento da curva y = x 2 8 - ln x 4 ≤ x ≤ 8
Determine os comprimentos das curvas nos Exercícios 55 e 56.56- x = y 4 2 - 2 ln y 4 , 4 ≤ y ≤ 12
Três partículas tendo massas 4, 2 e 7 kg estão no eixo x, nos pontos com coordenadas -5, 4 e 2 respectivamente, onde a distância é medida em metros. Ache o centro de massa do sistema.