Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 42
Considere um fabricante de latas quadradas que vai utilizar pedaços de folhas-de-flandres de kcm de lado, cortando-se quadrados de lado x cm das pontas e dobrando.
a): Se xcm for o comprimento dos lados dos quadrados a serem cortados, expresse o volume em centímetros cúbicos como uma função de x.
b): Qual o domínio da função ?
c): Prove que a função é contínua em todo seu domínio.
Passo 1
Letra a):
Antes de tudo, temos que entender o procedimento de corte e confecção da caixa. Repare esta imagem:
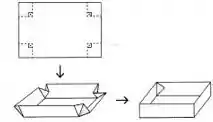
Ela ilustra uma folha, na qual foram cortados quadrados de mesmo comprimento e dobrou-se a folha de forma a obter uma caixa.
Assim, sendo Kcm uma constante real positiva fixada (ou seja, não vai variar que nem a incógnita x) o tamanho da folha e sendo X cm o valor do lado do quadrado, perceba que a altura da caixa é exatamente o lado do quadrado e a base é formada por (comprimento – 2x) e (largura – 2x).
Portanto, nosso volume será dado por
Passo 2
Letra b):
Repare que, da natureza do problema, o lado do quadrado não pode ser negativo e muito menos ultrapassar da metade de K (tendo em vista que são 2 quadrados cortados pra cada lado).
Assim, nosso domínio será:
Passo 3
Letra c):
Como nossa função V é produto de 3 polinômios de grau 1, é uma função polinomial, que sempre é contínua em todo o domínio.