Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 52
Considere a função
- Mostre que para
- Mostre que para
- O que você pode concluir sobre o ?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Primeiramente queremos mostrar que a função será para os seguintes valores de :
Em seguida, queremos mostrar que a função será para os seguintes valores de :
Para demonstrar essas duas afirmações, deveremos analisar o significado da tangente no que diz respeito ao círculo trigonométrico:
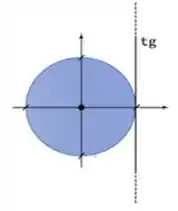
Por fim, deveremos analisar e explicar o seguinte limite:
Observação: Perceba que as duas demonstrações acima os números se tornam cada vez menores. Por conta disso a questão quer que a gente analisa bem esse limite.
Agora bora lá!! 😉
Passo 2
Para qualquer número , inteiro e positivo, temos que, se:
Então:
Sendo assim, para valores inteiros e positivos de :
Isso pode ser explicado na figura abaixo, pois sempre irá ser um dos dois quadradinhos vermelhos, os quais coincidem com o zero da tangente:
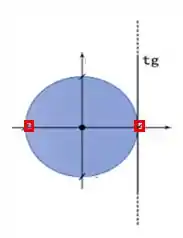
Passo 3
O círculo trigonométrico acima nos ajuda a visualizar que para os valores inteiros positivos de a tangente é zero.
Agora mostraremos que para
Para qualquer valor inteiro e não negativo de , a expressão que descreve o incremento no valor de é:
Sendo assim:
Sendo assim, só estaremos percorrendo a função tangente no círculo trigonométrico no mesmo passo da sua periodicidade , podemos resumir a última expressão a:
Passo 4
O que podemos concluir a respeito de:
Do passo 1 temos que quando .
Do passo 2 temos que quando .
Dessa forma, podemos concluir que o limite:
Não existe, devido a teoria fundamental do limite, uma vez que não se aproxima de um número fixo quando .
É possível verificar o comportamento da função no ponto através do gráfico a seguir para confirmar nossa suposição:
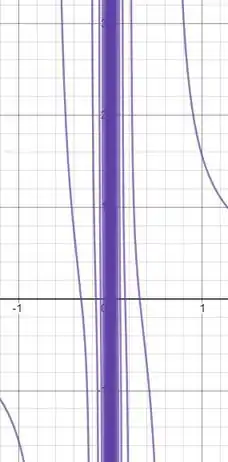
Perceba que é impossível definir o limite quando .
Resposta
Demonstração